Perättäinen eli “sekvenssi”säätö
Ensimmäinen artikkeli/4/ käsitteli tilannetta, jossa on yksi tunnettu tekijä, säätäjä, jolla on suoraan vaikutus keskiarvoon ja “toisto”näyte prosessista saadaan nopeasti.
Artikkelissa esitin Grubbsin asetussäännön ja erityisesti tilastollisen näytemäärän ja rajan (suunnitelmat A-H), jolloin säädön voi tehdä ilman suurta virheellisten tuotteiden riskiä. Säädön valintaan vaikuttaa ensisijassa prosessin suorituskyky Cp ja virheprosentti. Taulukossa 1 pahimman tapauksen (riski n. 3 %) virhemäärät.

Virhemääriä tarkasteltaessa ja valittaessa asetussuunnitelmaa on huomioitava myös tuotteen tai palvelun monimutkaisuus eli liitettävien osien tai palvelujen määrä, jotta voidaan onnistua ensimmäisellä kerralla kokonaisuutena. Tätä onnistumisen todennäköisyyttä kutsutaan “läpivyörytetyksi saannoksi” (Rolled throughput yield). Tätä onnistumista kuvaa seuraava taulukko 2.
Taulukossa oletetaan, että prosessin keskiarvo on asetettu täydellisesti tavoitearvoon (≈vihreät asetukset). Jos prosessin suorituskyky on Cp=1 ja säätö suoritettu H-suunnitelmalla, 10 komponentin kokonaisuus on todennäköisesti ensimmäisellä kerralla oikein 50 % todennäköisyydellä. Jos prosessin suorituskyky on Cp=2 ja käytetty suunnitelmaa A, on 10 komponentin kokonaisuus ensimmäisellä kerralla oikein 99,997 % todennäköisyydellä.

Tässä toisessa artikkelissa käsitellään perättäistä (sequential) säätötapahtumaa, joka sopii erityisesti raskaiden prosessien säätöön, joissa prosessin läpimenoaika on pitkä ja toisaalta rikkoutuvia tuotteita tuottavien prosessien säätöön. Tällä menettelyllä minimoidaan “pitkän” tai “rikkovan” säädön aikana syntyvien virheellisten tuotteiden (virheellisen prosessin keskiarvon) aiheuttamat kustannukset siinä määrin kuin data ja sattuma sen sallii.
Artikkelissa käsitellään myös esivalvonta ohjausta (precontrol), jossa on yhdistettynä asetusmenettely ja ohjaus samassa “paketissa”. Sopii erityisen hyvin asetuskeskeiseen tuotantoon kappaletuotantoon. Vaatii, että Cp≥1.
Kolmannessa artikkelissa käsittelen tilannetta, jossa ei ole tunnettua selkeää säätävää tai ohjaavaa tekijää tai tekijöitä on lukuisia, joiden avulla prosessia säädetään.
Prosessin keskiarvon asettaminen perättäisellä säädöllä
Jos prosessin rakenne tai mittaukset ovat sellaiset, että yksittäistä mittausarvoa joudutaan käyttämään prosessin keskiarvon asettamiseen, silloin prosessin keskiarvo on aina tavoite ±2,88σ (σ=standardipoikkeama). Käsittelin sigman määrittämistä edellisessä artikkelissa Osa I/4/. Jos prosessin keskiarvolle asetettu vaatimus on tätä tiukempi, silloin tarvittava datamäärä on kerättävä usean tunnin tai jopa päivien aikana ja toteutettava säätö “sekvenssi”säätönä.
Ei ole mitään mahdollista saada prosessin keskiarvoa lähemmäksi tavoitetta 97 % luotettavuudella kuin 2,88σ yhdellä näytteellä, vaikka yleisesti näin uskotaankin. Tyypillisiä tilanteita syntyy prosesseissa, joissa mittaustuloksen ottaminen tai analysointi on hidasta ja tarvitaan esim. laboratorioanalyysi – kemialliset ja lujuusanalyysit, hitaat prosessit jne. Miten kiertää ongelma?
Miksi prosessin keskiarvolla on vaikea saavuttaa tavoitetta, nominaalia eli tuotekeskiarvoa? Edellisessä jaksossa käsiteltiin tilannetta, jossa otetaan yksi näyte – suunnitelma A. Suunnitelman A kriittinen etäisyys Δσ=1,44σ, kun n=1. Prosessin keskiarvo on välillä nominaali ± 1,44σ noin 70 % ajasta ja ±2,88σ 97 % ajasta, kun käytetään A-suunnitelmaa.
Mitä tapahtuu, jos operaattori päättää käyttää pienempää arvoa kuin 1,44σ päätöskriteerinä? Onnistuuko hän säätämään prosessin keskiarvon lähemmäksi tavoitetta, nominaalia?
Oletetaan, että operaattori käyttää säätöpäätökseen kriteeriä Δσ = 0,84 kun hän ottaa yhden mittauksen n=1. Tällä hän uskoo säätävänsä prosessin lähemmäksi nominaalia, mutta todellisuudessa tapahdu, että prosessin keskiarvo on 88 % todennäköisyydellä ±1,68σ nominaalista. Tämä vastaa alkuperäistä tilannetta, jossa keskiarvo on 70 % todennäköisyydellä ±1,44σ nominaalista. Todellinen seuraus on siis lisääntyvä määrä turhia säätöjä. Turhien säätöjen osuus kasvaa 15%:sta 40 % samalla kun vaihtelu kasvaa.
Edellä olevaa peukalointia ja parantelua demonstroidaan usein Demingin suppilokokeella tai Quincunx -nimisellä kehitetyllä laitteella. Stabiili tila on punaisen viivan kohdalla (3 sigma)!
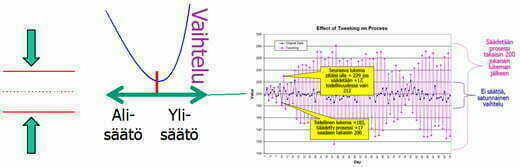
Prosessin säätäminen tarkoittaa aina “epästabiilin” tilan luomista, ylisäätöä. Kysymys on alfa- ja betavirheiden suuruuksista. Säädössä alfavirhe p=0,15 on yleisesti hyväksytty taso, kun stabiilin keskiarvon säilyttämisessä (SPC) p=0,0027. Alfavirhe 0,15 tarkoittaa karkeasti, että on 15 % todennäköisyys, että säätö heikentää tulosta.
Miten voimme säätää prosessin keskiarvon lähemmäksi nominaalia käyttämällä vain yhden mittauksen tuloksia? Perättäinen asetusmenettely.
Asettamisen oletukset: Oletetaan, että tuotteen/palvelun ominaisuuden keskiarvo on pidettävä lähellä jotain arvoa (tavoite, nominaali). Jokaisen mittauksen jälkeen arvioidaan prosessin keskiarvoa niin tehokkaasti kuin data sen mahdollistaa.
Tämä menettely on monimutkaisempi ja vaatii laskentaa verrattuna asetussuunnitelmiin A-H, jossa lasketaan näytteen (n mittauksen) keskiarvo ja verrataan keskiarvoa kriittiseen mittaan nominaali± Δσ. Tästä tehdään päätös säätää tai ei. Säätö tapahtuu aina ylisäädön puolelta. Jos ylisäätö on liian suurta, tapahtuu värähtely eli hajonnan kasvua!
Perättäinen säätö on kuitenkin välttämätön, kun mittaukset/analyysit ovat aikaa vieviä tai kalliita. Tällöin “ylimääräinen” työ on vaivan arvoinen ja säätöprosessin, sekvenssin, aikana väärästä säädöstä johtuva hukka on minimissä.
Prosessin stabiilisuus
Koko menettely, jolla säädetään prosessin keskiarvoa, voi olla hyödytön, jos prosessi itsessään ei ole ohjauksessa. Silloin prosessilla ei ole yhtä keskiarvoa vaan lukuisia eri keskiarvoja ja hajontoja.
Jos edellä oleva operatiivinen stabiilisuus on voimassa, voidaan aikaisemmat mittaukset yhdistää viimeiseen mittaukseen ennen viimeisen mittauksen avulla tehtävää prosessin keskiarvon arviointia. Koska aikaisemmin mitatut arvot yhdistetään viimeiseen, tästä seuraa, että kriittinen Δσ muuttuu sen mukaan kun informaation määrä kasvaa. Kuvassa 2
Asetuksen perusmenettely
Perusmenettely prosessin tavoitteen – säätöjen – asettamiseksi on erittäin yksinkertainen:
- Aseta prosessin keskiarvon tavoite (<2Δσ), tee säätö (huom. prosessin keskiarvotavoite on eri asia kuin nominaalitavoite T)
- Mittaa yksi havainto ominaisuudesta, jota asetat (näyte)
- Vertaa arvoa perättäisen näytetaulukon kriittiseen arvoon Δσ.
– Jos arvo on perättäisen kriittisen arvon sisäpuolella, ota uusi havainto ja liitä havainnon arvo aikaisempiin arvoihin.
– Jos havainto on kriittisen arvon ulkopuolella, säädä prosessia ja aloita säätöpolku alusta. Askel 1.
Säätöpolkua kulkiessasi, laske aina edelliset mittaukset mukaan keskiarvoon ja vertaa tätä ko. kriittiseen arvoon. - Jatka näin, kunnes päädyt asettamaasi VÄLIIN nominaali ± Δσ
Mitkä ovat optimaaliset asetusarvoyhdistelmät ja niiden luotettavuusarvot?
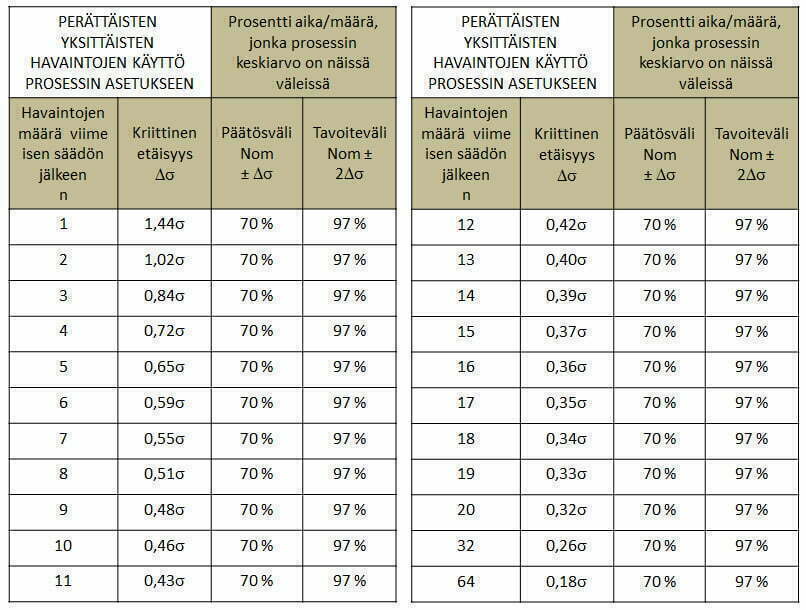
Seuraavassa taulukossa on annettuna optimaaliset perättäiset havaintojen määrät viimeisen säädön jälkeen ja kriittiset etäisyydet Δσ. Taulukossa on suunnitelman takaamat keskimääräiset ajat (määrät), jonka ajan prosessi on annetulla välillä nominaalin ympärillä.
Suunnitelman valinta 2Δσ perusteella
Kuinka organisaatio (tuotantopäällikkö/insinööri tai laatupäällikkö/insinööri) määrittelee käytettävän suunnitelman 2 ∆σperusteella (näytemäärän n ja kriittisen etäisyyden Δσ nominaaliarvosta)? Valinta ei poikkea Osa I:ssä esitettyihin valintaperusteista. Kysymys on ensisijassa virheellisen tuotteen tai tuotekokonaisuuden (kokoonpanon) syntymisen riskihallinnasta.
Päätös suunnitelman vallinnasta voi perustua mm. seuraaviin seikkoihin:
- Prosessin keskiarvo on määritetty suunnittelu- tai asiakasvaatimuksissa erillisenä toleranssista esim. keskiarvo: nominaali ± 2,05 ja toleranssi: nominaali ±3
- Asiakasvaatimus on sidottu Cpk tai Ppk indeksiin toleranssin lisäksi. Autoteollisuuden standardi PPAP (AIAG: Production Part Approval Process) määrittelee prosessivaatimukseksi Ppk>1,67
- Asiakas vaatii tietyn minimisaannon eli virheprosentille on asetettu raja joko AQL tai LTPD-muodossa. Liittyy siis erien hyväksymistarkastukseen.
- Huonon laadun (virheellisten tuotteiden) määrälle on asetettu katto tai maksimi. Six Sigma -vaatimus <3,4 ppm.
- Laadun hävikkikustannus tai materiaalihävikki on saatettava tietyn tason alapuolelle esimerkiksi erilaiset ympäristöpäästöt.
- Toleranssisuunnittelusta tulevat erilaiset vaatimukset
Virhemääriä voidaan arvioida seuraavan nomogrammin avulla, joka oli esillä tarkemmin I-osan artikkelissa.

Esimerkki käytöstä:
Kun vain yksi mittaus on käytettävissä viimeisen säädön jälkeen, vertaat tätä arvoa nominaaliarvoon ja säädät, jos arvo poikkeaa enemmän kuin 1,44σ nominaaliarvosta.
Kun kaksi mittausta säädön jälkeen on käytettävissä, yhdistetään nämä mittaukset keskiarvoksi. Jos tämä keskiarvo on suurempi kuin 1,02σ nominaaliarvosta, säädetään prosessin keskiarvoa.
Kun kolme mittausta säädön jälkeen on suoritettu, yhdistetään nämä mittaukset keskiarvoksi ja jos tämä keskiarvo on suurempi kuin 0,84σ nominaalista, suoritetaan säätö.
Näin jatketaan siihen asti, kunnes saavutetaan asetettu 2Δσ. Ja tästä johdettu n. Tällöin kriittinen mitta on puolet tavoitteesta 2Δσ/2=Δσ ja säätöä ei saa suorittaa. Tässä vaiheessa on kerätty perättäin riittävästi dataa keskiarvoon, jotta voidaan varmistaa prosessin keskiarvon olevan halutulla etäisyydellä nominaalista.
Taulukon n ja Δσ on suunniteltu niin, että kun päätös “EI TEHDÄ SÄÄTÖÄ” on tehty perustuen n arvon keskiarvoon, prosessin keskiarvo on 70 % ajasta ± Δσ nominaaliarvon välissä. Prosessin keskiarvo on 97 % ajasta välissä nominaali ± 2Δσ
Tarkastellaan esimerkiksi tilannetta, jossa operaattorin on säädettävä prosessin keskiarvo yhden standardipoikkeaman sisään nominaalista (2Δσ=1σ) Operaattorin on noudatettava edellä olevaa menettelyä kunnes hän päätyy 9 havainnon säätämättömään ketjuun n=9. Silloin hän voi olla vakuuttunut, että prosessin keskiarvo on 2Δσ=0,96σ nominaaliarvosta. Keskimäärin 70 % ajasta prosessin keskiarvo on Δσ=0,48σ sisällä nominaaliarvosta.
Esimerkki: Metallinauhan valmistus – perättäinen (sequential) asettaminen
Valssattua ja muotoon puristettua nauhaa valmistetaan jatkuvalla tuotantolinjalla. Nauhan mitta on kriittinen materiaalista ja valssiasetuksesta. Nauhan kriittinen nominaalimitta on 5,250 mm. Prosessin ohjauskortti osoittaa, että nauhakelan vaihtuessa tapahtuu usein mitan muutos.

Tämän perusteella päätettiin, että kone on säädettävä jokaisen kelavaihdon yhteydessä. Säätömenettelyksi valittiin perättäinen menettely niin, että prosessin keskiarvon on oltava yhden sigman sisällä nominaalimitasta. Tällä minimoidaan prosessin asetussekvenssin aikana mahdollisesti syntyvää hukan määrää, koska prosessin luonteen vuoksi mittauksia ei voida tehdä välittömästi peräkkäin (eivät ole riippumattomia ja prosessin satunnainen vaihtelu ei tule mittaustuloksiin oikein. Vaihtelu inflatoituu!)
Prosessin stabiilisuus testattiin I-MR -kortilla, josta saatiin sigma =0,0016.
Tämä perusteella laadittiin Excel-lomake, joka auttaa datan keräämisessä, laskennassa ja säädön kirjauksessa.

Säädön lopetuspiste on merkitty punaisella lomakkeeseen 9-perättäisen havainnon päähän säädöstä, koska prosessin keskiarvon tavoite on korkeintaan 1 sigma nominaali arvosta, 2Δσ=0,96σ.
Kelan vaihdon jälkeen operaattori aloittaa säädön. Heti ensimmäinen mittaus on päätösvälin ulkopuolella. Seuraa säätö alaspäin ohuemmaksi.

Kun säätö on suoritettu, aloitetaan uusi lomake alusta.

Edelleen prosessi osoittaa, että säätöä on suoritettava alaspäin. Operaattori aloittaa uuden lomakkeen.
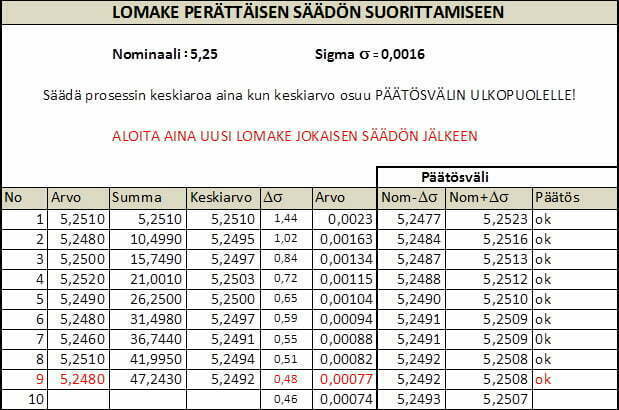
Nyt operaattori pääsi koko sekvenssin läpi, vaikka keskiarvo on vasemmalla tavoitteesta, operaattori päätti, että prosessin keskiarvo on halutulla välillä (±1sigma) nominaalista. Osaotoksen perusteella osoittautui, että prosessin keskiarvo oli 5,2505.
On erikseen harkittava, voiko niitä tuotteita käyttää, jotka tapahtuivat ennen kuin saatiin vahvistus prosessin keskiarvon vaatimustenmukaisuudesta.
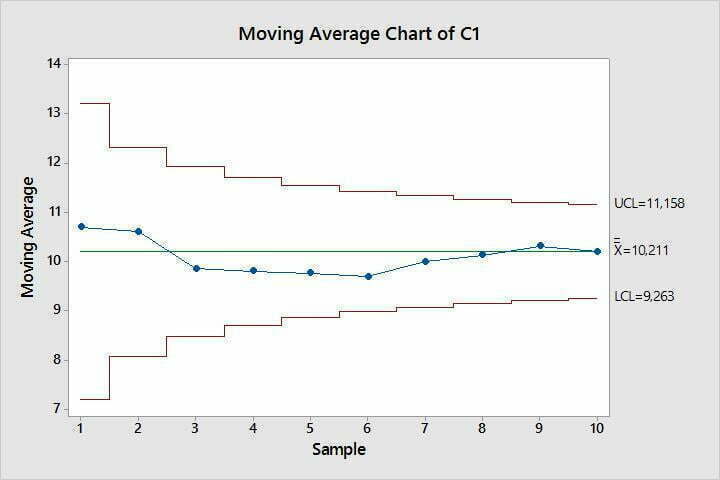
Sekvenssisäädön toteuttaminen Minitabilla
Minitabissa on mahdollista käyttää Stat-> Control Charts->Time-Weighted Charts Moving Average. Tämä SPC-työkalu on tarkoitettu pienien keskiarvomuutosten havaitsemiseen. Tätä voi käyttää myös sekventiaaliseen prosessin keskiarvon asettamiseen pienin muutoksin.
Tarkastellaan metallinauhaesimerkin mukaista tilannetta, jossa prosessi on asetettava 1 sigman sisään nominaalista. Taulukon 1 mukaan tarvitaan 9 näytteen liukuva keskiarvo.

Säätö I: Analyysi

Punainen piste ei ole rajojen sisällä. On suoritettava säätö alaspäin ja aloitettava uusi sarja. Koska oli yksi piste, käytettiin etukäteistietoa sigmasta.
Säätö II
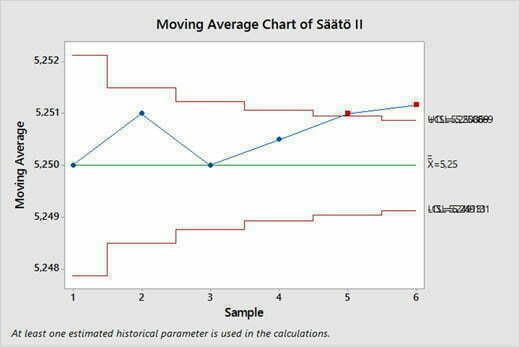
Prosessi on säädettävä jopa viidennen näytteen jälkeen. Jos käytetään etukäteistä sigmaa 0,0016, päätös tapahtuu 6 näytteen keskiarvon perusteella. Minitabissa on automaattinen updates, jolloin tulokset voi sijoittaa sitä mukaa kun ne syntyvät ja Minitab täydentää kuvaa automaattisesti.
Säätö III

Prosessin keskiarvo on saavuttanut 1 sigman etäisyyden nominaalista. Prosessin keskiarvo on “rajalla”, mutta tässä tapauksessa päätettiin tuotantoa jatkaa ja siirtyä stabiilin tilan ylläpitoon SPC-kortia käyttämällä ja havaitsemalla erityissyyt, jos niitä ilmenee.
Esivalvontakortti (Pre-control)
Toinen sekvenssi-asetusmenetelmiin ja ohjaustekniikoihin kuuluva tekniikka on esi-valvonta, jonka kehitti Dorian Shainin johdolla Frank Satterthwaite 1954/2/. Tekniikka on yksinkertainen ja helppo soveltaa ja perustuu toleranssirajoihin.
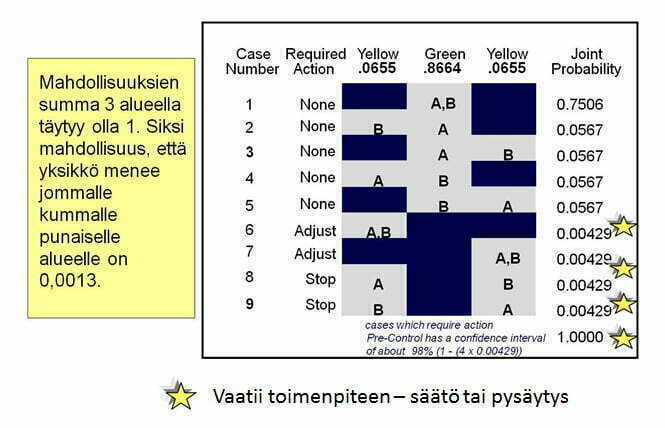
Esi-valvonta perustuu neljään yksinkertaiseen sääntöön:
- Esi-valvontarajojen luominen (rajat)
- Prosessin suorituskyvyn pikamääritys
- Esi-valvonta tuotannossa: Näytekoko; jatkaminen/pysäytys
- Näytetaajuus
Asetuksen kannalta kiinnostavaa on tekniikkaan sisältyvä asetus, jolla taataa, että prosessin suorituskyky on riittävä ja virheellisten tuotteiden määrä korkeintaan n. 2%.
1. Esivalvontarajojen luominen
Jaa toleranssiväli (tai ohjausrajaväli, jos Cp>1) neljään yhtä suureen vyöhykkeeseen, joista kaksi keskimmäistä muodostaa vihreän vyöhykkeen. Kaksi seuraavaa keltaisen vyöhykkeen ja näiden ulkopuolella oleva alue on punainen.

2. Prosessin suorituskyvyn pikamääritys
Määritä prosessin kyvykkyys ottamalla 5 perättäisen kappaleen näyte.
Kaikkien osien on oltava vihreällä vyöhykkeellä, jotta voidaan todeta prosessin olevan kyvykäs ja ohjauksessa. Jos yksi osa on vihreän vyöhykkeen ulkopuolella prosessi ei ole kyvykäs tai ei ole ohjauksessa.
Asetuksen oikeellisuus siis testataan 5:llä perättäisellä kappaleella. Jos ne kaikki ovat toleranssin puolikkaan sisällä, asetus on ok. Jos ei, on tehtävä uusi asetus tai DOE/Six Sigma, jolla suorituskykyä parannetaan. Kuvassa todennäköisyys Cpk:n funktiona, että 5 perättäistä näytettä osuu vihreälle vyöhykkeelle.

3. Esi-valvonta tuotannossa: Näytekoko; jatkaminen/pysäytys
Aloitetaan tuotanto ja otetaan kaksi perättäistä yksikköä edeltä käsin määritetyn taajuuden perusteella (määritellään askeleessa 4 paremmin) ja noudatetaan seuraavia sääntöjä.
- Molemmat osat ovat vihreällä vyöhykkeellä => tuotanto jatkuu
- Yksi osa on vihreällä ja yksi osa on keltaisella vyöhykkeellä => tuotanto jatkuu
- Molemmat osat ovat samassa keltaisessa vyöhykkeessä => säädä prosessin asetus
- Osat ovat eri keltaisilla vyöhykkeillä => pysäytä tuotanto ja tutki vaihtelun syyt
- Jompi kumpi on punaisella vyöhykkeellä => pysäytä tuotanto ja tutki vaihtelun syyt kun prosessin on säädetty, askel 2 on toistettava aloitettaessa tuotanto
4. Näytetaajuus
Määritä näytetaajuus jakamalla keskimääräinen kahden pysäytyksen välinen aika 6:lla.
Esivalvonta perustuu tilastolliseen todennäköisyyteen, jossa virheellisen päätöksen todennäköisyys on 2 %. Ennakkoehto todennäköisyydelle on, että prosessi on kyvykäs rajoihin (5 kpl vihreällä).
Yhteenveto
Keskiarvon säätäminen oikein on keskeistä asetettaessa niin palvelu- kuin tuoteprosesseja, niissä olevia linjoja, koneita ja jopa erilaisia menettelyjä.
Silloin kun säätö voidaan toteuttaa yhdellä muuttujalla, säätimellä, on tiedettävä kuinka monta näytettä on otettava joko samalla kertaa tai perättäin sopivien jaksojen päästä. Lasketusta keskiarvosta voidaan päätellä kriittisen arvon Δσ avulla, onko säätö suoritettava vai ei. Jos säädön suorittaa pienemmästä arvosta kuin taulukko osoittaa, seuraa turhaa työtä ja lisää vaihtelua.
Säätö/asetusmenettelyt takaavat yritykselle, että operaattorit toimivat niin, että prosessin tuottamat virheet ovat minimissä tai jopa eliminoidut. Mitä huonompi/pienempi on prosessin suorituskyky Cp, sitä vaativampaa on prosessin keskiarvon säätäminen ja sitä tärkeämpää on käyttää oikeita tilastollisia säätö- ja asetusmenetelmiä.
Prosessin stabiilisuuden säilyttäminen on aina välttämätöntä ja näin SPC -ohjauskorttien käyttö on enemmän kuin suotavaa. Ohjauskortit ilmaisevat epästabiilisuuden ja erityissyyt, jotka olisi poistettava. Samalla erityissyyt ovat mahdollisuus parantaa prosessia.
Artikkelisarjan kolmannessa osuudessa käsitellään suorituskykyä ja sen parantamista. Säätämällä vain prosessin keskiarvoa sillä on vain rajalliset, joskin merkittävät mahdollisuudet, parantaa laatua, vähentää virheitä ja näin myös lisätä tuottavuutta.
Lähteet:
- Donald J.Wheeler, Davis S. Chambers: Understanding Statistical Process Control, SPC Press, 1986
- Keki R. Bhote, Adi K. Bhote: Word Class Quality – Using Design of Experiments to Make it Happen, 2000
- Minitab 18
- Artikkeli: Eero E. Karjalainen: Prosessin ja työkoneen säätäminen ja asettaminen – OSA I, 2017
Lue koko artikkelisarja:
Tilaa uutiskirje
Liity postituslistalle ja saat uusimmat artikkelit suoraan sähköpostiisi.
Tämä lomake on suojattu Google reCAPTCHA:lla. Lue tietosuojaseloste ja käyttöehdot.
Liittymällä postituslistalle hyväksyt Quality Knowhow Karjalainen Oy:n tietosuojaselosteen ja Quality Knowhow Karjalainen Oy voi lähettää sinulle ajankohtaisia artikkeleita, videoita sekä tietoa ja tarjouksia kursseista, kirjoista sekä ohjelmistoista.
