Mihin koira karvoistaan pääsisi?
Nyt ei kuitenkaan puhuta koirista, vaan vähintään yhtä mukavasta asiasta; tilastotieteestä. Monet ovat varmaan törmänneet tähän ihanuuteen koulussa, ja sen jälkeen pyrkineet unohtamaan kaiken kuulemansa aiheesta. Vanha kansa toisaalta tiesi jo muinoin kertoa ”valhe, emävalhe, tilasto”, eli tiettyä epävarmuutta aiheen ympärillä varmasti on. Tässä artikkelissa on tarkoitus tutustua asiaan prosessien näkökulmasta, kuten ehkä tiedätte, kaikki työ tapahtuu prosesseissa.
Mikä ero sitten on siinä koulussa opitussa tilastotieteessä verrattuna tähän prosessien näkökulmaan?
Tilastotiede voidaan jakaa esimerkiksi näihin kolmeen kategoriaan:
- Kuvaileva (descriptive): ”Mitä voin sanoa tietystä tuotteesta / potilaasta?”
- Luetteloiva (enumerative): ”Mitä voin sanoa tietystä tuoteryhmästä / potilasryhmästä?”
- Analyyttinen (analytic): ”Mitä voin sanoa prosessista, joka tuotti tämän tuoteryhmän / potilasryhmän ja kyseiseen ryhmään liittyvät tulokset?”
Koulujen tilastomatematiikan / tilastotieteen kurssit katsovat asiaa kuvailevasta ja luetteloivasta perspektiivistä. Analyyttisen tilastotieteen kuuluu olennaisena osana tulosten tuottaneen prosessin tunteminen. Kaikki kolme tapaa ovat sinänsä toimivia, mutta analyyttisen käsittelyn puuttuminen saattaa johtaa virheellisiin tulkintoihin ja jopa toimenpiteisiin. Analyyttinen käsittely antaa meille mahdollisuuden käsitellä tulevaisuutta, eli ennustaa (tietyissä rajoissa). Eero E. Karjalainen on käsitellyt aihetta tarkemmin muun muassa artikkelissaan Numeeriset ja analyyttiset tutkimukset.
Tutkitaan asiaa tarkemmin esimerkin kautta. Apuna käytetään (kuvitteellista) kolmesta eri sairaalasta kerättyä dataa hoitojaksojen pituuksista (Length of Stay – LOS), datan voit ladata xlsx-tiedostona tästä. THL määrittelee hoitojakson pituuden seuraavasti: ” Hoitojakson pituus lasketaan hoidon lähtö- ja tulopäivän erotuksena. Näin ollen hoitojakson pituus voidaan tulkita hoidossa vietettyjen öiden lukumääränä. Poikkeuksen muodostavat yhden päivän kestäneet hoitojaksot (esimerkiksi päiväkirurgia), joiden pituudeksi kirjataan siis yksi päivä.” Data pitää sisällään sairaalakohtaisesti tiedon kunkin viikon keskimääräisestä hoitojakson pituudesta.
Meitä kiinnostava kysymys on: ”Onko sairaaloiden välillä eroa?”
Kuvaileva ja luetteloiva lähestyminen
Lasketaan ensin muutamia niin sanottuja tunnuslukuja datasta, eniten käytetty tunnusluku on varmaankin kaikille tuttu keskiarvo. Ja mukana myös ohje miten teet saman Minitab:lla.
Tunnuslukuja saadaan laskettua vaikkapa Display Descriptive Statistics -komennolla (Stat>Basic Statistics> Display Descriptive Statistics). Minitab:lle pitää vain kertoa sarakkeet, joita laskennan pohjana käytetty tieto löytyy, ja jos haluaa itse päättää mitä lasketaan, niin siihen voi vaikuttaa ’Statistics…’ painikkeen kautta.
Tuloksena saadaan alla oleva taulukko, mutta mitä se kertoo meille? Ovatko sairaalat erilaisia vai samanlaisia hoitojakson pituuden suhteen?
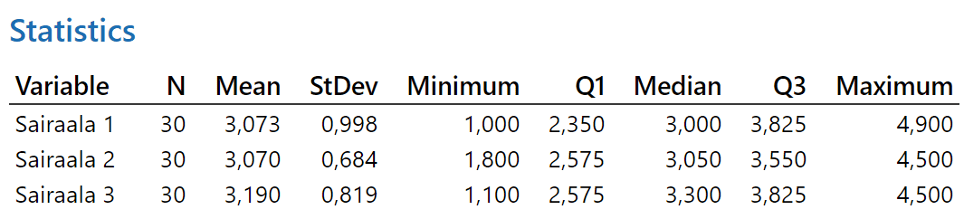
Keskiarvot (Mean) eri sairaaloilla ovat saman kaltaisia. Mikään ei pomppaa silmille. Käsi ylös, kuka jo julistaisi sairaalat samanlaisiksi? Eihän teillä tehdä päätöksi pelkän keskiarvon perusteella? Mitä muuta voidaan tehdä? Piirretään datasta kuva!
Yksi mahdollinen kuva on Minitab:n Dotplot (Graph>Dotplot). Kerrotaan ohjelmalle, mitä sarakkeita käytetään ja jos halutaan kaikki sairaalat samaan kuvaan, tämän voi tehdä ’Multiple Graphs…’-painikkeen alta.
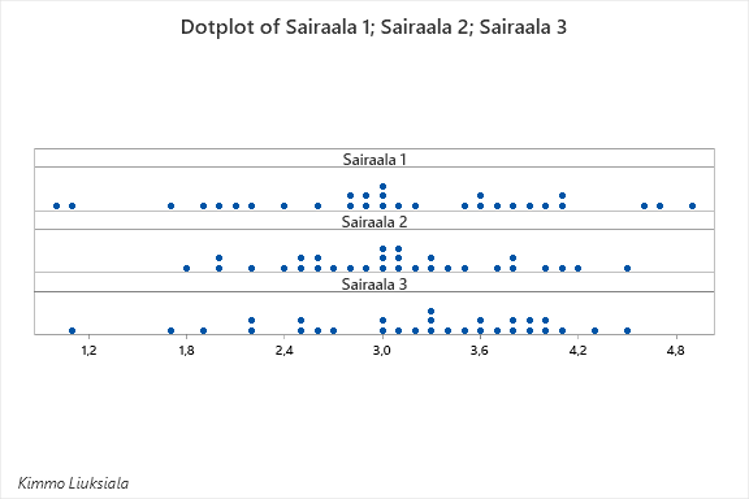
Kuva näyttää tältä, ei vieläkään eroa näkyvissä.
Löytyykö sairaaloiden hoitojaksojen pituuksien keskiarvojen välille tilastollisesti merkittävää eroa? Miten tätä voidaan tutkia? Menetelmä tottelee nimeä varianssianalyysi eli ANOVA (Analysis of Variance) ja meille riittää tässä tilanteessa ns. yksisuuntainen (One-Way ANOVA) versio aiheesta.
Dataa on sairaalakohtaisesti sen verran paljon (n=30), ettei ANOVA:n vaatimus havaintojen normaalijakautuneisuudesta tuota haasteita, mutta tarkastetaan tämä kuitenkin. Minitab:n normaalisuustesti (Stat>Basic Statistics>Normality Test…) täytyy tehdä kullekin sairaalalle erikseen.
Normaalisuustesti kertoo meille, ettei minkään sairaalan osalta löydetty todistusaineistoa sille, etteivätkö hoitojaksojen pituudet voisi olla kotoisin normaalijakaumasta.
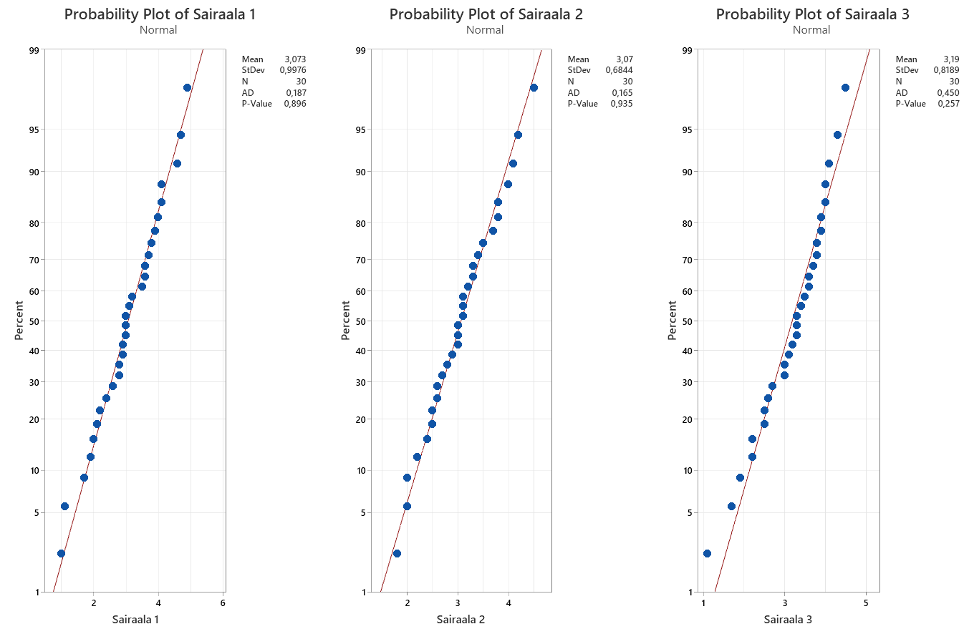
Normaalisuustestin perusteella saadun kuvan tulkinta menee seuraavasti: Mikäli siniset pisteet (yksittäiset havainnot datassa) osuvat kohtuullisen hyvin punaisen viivan (normaalijakauman kertymäfunktio), voidaan todeta normaalijakauman kuvaavan havaintoja kohtuullisen hyvin. Ja sama tulkinta voidaan tehdä testien p-arvojen perusteella; vain jos saatu p-arvo on pienempi kuin 0,05 olisi meillä todisteita siitä, etteivät havainnot olisi kotoisin normaalijakaumasta.
Nyt voisimme jo edetä varsinaiseen sairaaloiden keskiarvojen vertailuun yksisuuntaisella varianssianalyysilla, mutta saamme testiin lisää tehoa, jos voimme todeta eri ryhmien (sairaaloilla) vaihtelun olevan samansuuruista. Tämähän pitää tietenkin testata (Stat>ANOVA>Test for Equal Variances…).
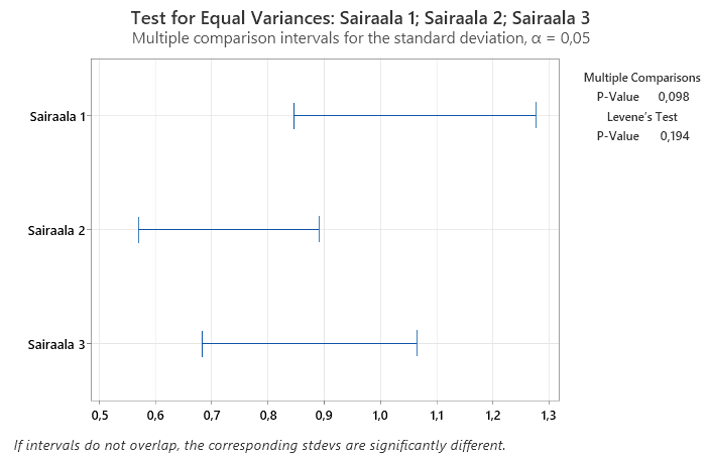
No onko vaihtelu samankaltaista eri sairaaloiden hoitojaksojen pituuksissa? Ei voida sanoa, etteikö olisi. Vertailuintervallit menevät päällekkäin ja testien p-arvot ovat suurempia kuin 0,05. Nyt ANOVA:n kimppuun (Stat>ANOVA>One-Way…)
Yksisuuntainen varianssianalyysi tutkii ovatko tekijän eri tasojen (Sairaala 1, Sairaala 2, Sairaala 3) keskiarvot samanlaiset (nollahypoteesi), vai löytyykö keskiarvojen välille tilastollisesti merkittävä ero (vaihtoehtoinen hypoteesi).

Varianssianalyysin tulokset löytyvät taulukosta:

Tekijällä (Factor) on siis kolme mahdollista tasoa (Sairaala 1, Sairaala 2 ja Sairaala 3) ja testin tulos löytyy taulukosta p-arvon kohdalta (0,822). P-arvo on suurempi kuin 0,05, joten emme voi niin sanotusti hylätä asetettua nollahypoteesiämme. Eli meillä ei ole riittävästi todisteita lausuaksemme, että eri sairaaloiden välillä olisi eroa.
Sama tulkinta voidaan tehdä graafisestikin. Kaikkien kolmen sairaalan keskiarvojen luottamusvälit menevät päällekkäin, eli eroa sairaaloiden välille ei löydy.
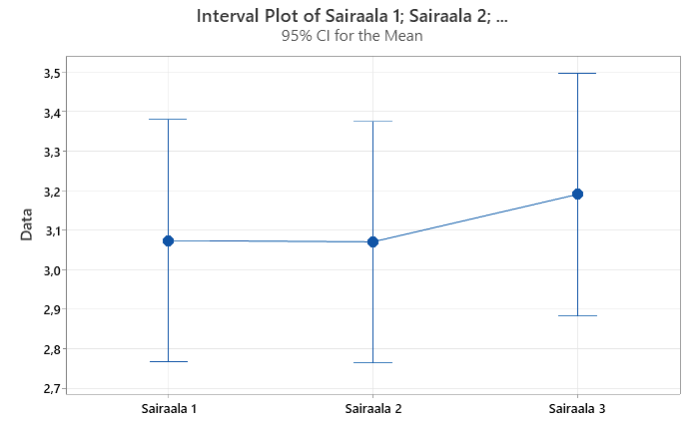
Kuvaileva ja luetteloiva lähestyminen eivät siis näytä löytävän eroa sairaaloiden välille. Mitä vielä voitaisiin tehdä?
Analyyttinen lähestyminen
Ennen kuin menemme eteenpäin, mieleen hiipii kolme kysymystä:
- Miten dataan liittyvät määrittely on tehty ja miten data on kerätty?
- Olivatko datan tuottaneet prosessit stabiileja (vakaita, ennustettavia)?
- Olivatko tähän mennessä tehdyt analyysit edes järkeviä?
Miten dataan liittyvät määrittely on tehty ja miten data on kerätty? Kaikki sairaalat käyttivät samaa määritelmää hoitojakson pituudelle ja syöttivät tiedot samaan järjestelmään. Joten tiedot ovat ainakin vertailukelpoisia näiden sairaaloiden välillä. Data on lisäksi kerätty aikajärjestyksessä.
Olivatko datan tuottaneet prosessit stabiileja? Tätä et välttämättä ollut vielä tullut ajatelleeksi! Kuten aiemmin mainittu, kaikki työ tapahtuu prosesseissa, kaikki tapahtuu niin sanotusti ”ajan yli”, eli aikajärjestyksessä. Ja tämä mahdollistaa datan tuottaneen prosessin stabiilisuuden arvioinnin. Piirretään siis data aikajärjestyksessä.
Yksinkertaisin versio tästä on aikasarjakuva (Time Series Plot) ja monesti yksinkertaisin riittää (Graph>Time Series Plot…).

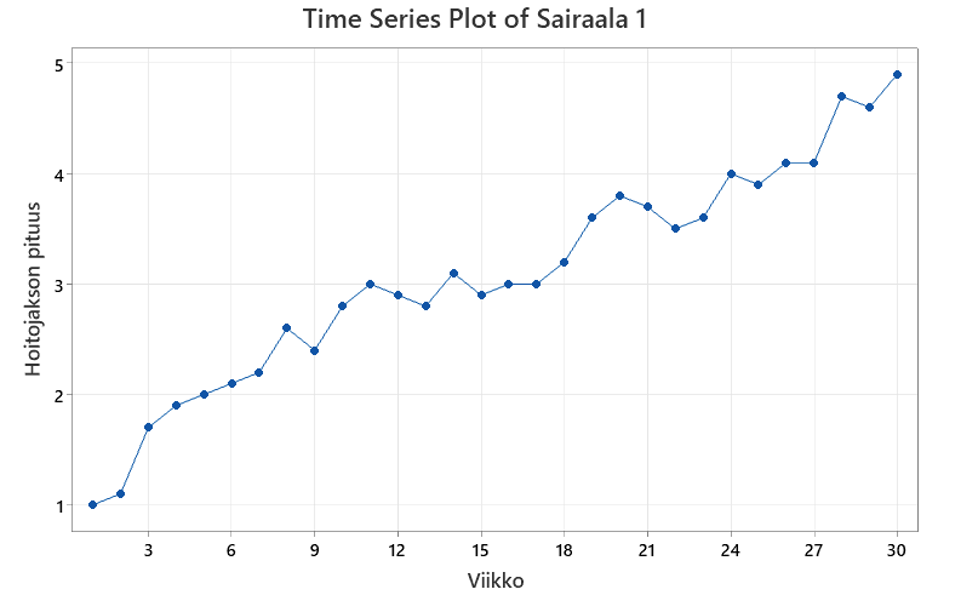
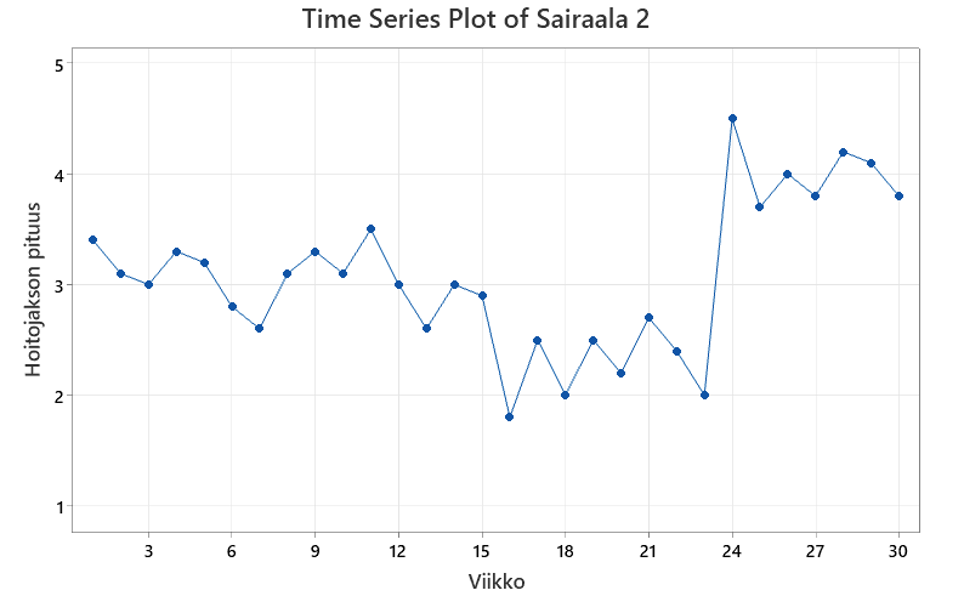

No, näkyykö eroja sairaaloiden välillä? Olivatko aikaisemmat analyysit järkeviä?
Mitä tarkoittaa keskiarvo sairaalan 1 tai sairaalan 2 osalta? Jos toinen jalka on melkein kiehuvassa vedessä ja toinen jäämurskassa, onko olo keskimäärin mukava? Sairaalan 2 osalta jos kysytään, ’mikä on hoitojaksojen keskiarvopituus?’, on sopiva vastakysymys ’millä aikavälillä?’ Sairaalalla 2 on kolme eri keskiarvoa, mitä voidaan sanoa tulevaisuudesta?
Sairaalan 1 hoitojakson pituuden viikkokeskiarvo kasvaa koko mittausjakson ajan, sairaala 2 hoitojakson pituuden keskiarvo muuttuu äkillisesti tasolta toiselle. Sairaalan 3 hoitojakson pituuden keskiarvo on ajan suhteen stabiili, vaikkakin vaihtelee paljon.
Pelkkä havaintojen piirtäminen aikajärjestykseen kertoo meille enemmän kuin aikaisemman menetelmät yhteensä, olisiko pelkkien keskiarvojen perusteella tehty oikeita päätöksiä?
Sairaala 3:n suhteen voimme tietenkin vielä hakea varmistuksen stabiilisuudesta ohjauskortin avulla. Stabiilisuushan tarkoittaa, että jos mikään ei muutu prosessi tuottaa myös tulevaisuudessa arvoja, joiden keskiarvo on sama kuin aikaisemmin ja ne vaihtelevat samojen rajojen sisällä. Emme siis pysty tarkasti kertomaan mikä on Sairaala 3:n hoitojakson pituus tiettynä viikkona tulevaisuudessa, mutta tiedämme mille välille se sijoittuu.
Ohjauskortit ovat nykyaikaisen laatutekniikan perustuksena tunnetun tilastollisen prosessinohjauksen (Statistical Process Control – SPC) työkaluja. Datamme on siinä muodossa, että oikea ohjauskortti tähän tarpeeseen on jatkuvalle datalle soveltuva yksittäisten havaintojen I-MR ohjauskortti (Stat>Control Charts>Variables Charts for Individuals>I-MR…).

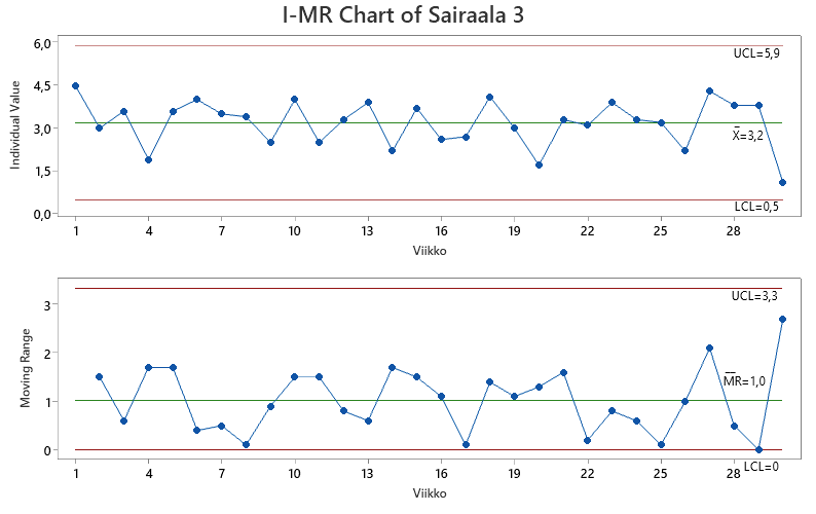
I-MR -ohjauskortti jakaantuu kahteen osaan:
- Alempi osa (Moving Range) kuvaa havainnosta seuraavaan hyppäyksen suuruutta.
- Ylempi osa (Individual Value) kuvaa yksittäistä havaintoa datassa, eli on itse asiassa aikasarja
Ohjauskorttien varsinainen lisäarvo muodostuu kuviin piirtyneistä rajoista, molemmissa kuvissa on yläohjausraja (Upper Control Limit) ja alaohjausraja (Lower Control Limit). Rajojen väliin jäävä alue kuvaa prosessin luonnollisen vaihtelun suuruutta, mitä laveammat rajat, sitä enemmän vaihtelua. Ohjausrajat lasketaan datan avulla, niitä ei anneta ulkoa. Ohjausrajojen voidaankin sanoa edustavan prosessin ääntä, prosessi kertoo meille, missä rajoissa se kykenee toimimaan.
Jos (ja Sairaalan 3 tapauksessa kun) kaikki havainnot ovat ohjausrajojen sisällä, niin prosessi on stabiili. Stabiilisuus ei sinänsä tarkoita, että tilanne olisi hyvä tai huono, se kertoo vain prosessin äänen. Stabiilissa tilanteessa puhutaan satunnaisesta vaihtelusta. Data ei pysty kertomaan meille yksittäistä syytä sille, että havainto sai juuri tietyn arvon, vaan havainto on aiheutunut tietyllä ajanhetkellä vaikuttaneista moninaisista tekijöistä ja näiden tekijöiden keskinäisvaikutuksista. Kaikissa prosesseissa on aina satunnasta vaihtelua. Yksittäiseen havaintoon ei tässä tilanteessa pidä reagoida.
Jos joku havainnoista olisi ohjausrajojen ulkopuolella, tai havaitsemme jotain muuta erityistä, sanotaan prosessin olevan ei-stabiili (epästabiili) näistä havainnoista käytetään nimitystä erityissyy. Sairaalan 1 havainnoissa näkyy trendi ja Sairaalan 2 havainnoissa selkeitä siirtymiä tasolta toiselle, eli molemmissa tapahtuu jotain erityistä. Tällaisissa tilanteissa on järkevää lähteä etsimään yksittäistä syytä tapahtumalle.
Analyyttisen lähestymisen ero verrattuna ”perinteisiin” on aika. Prosessin tuotos (ulostulo) vaihtelee ajan yli. Prosessin ulostulo on seurausta siihen vaikuttavista tekijöistä (sisäänmenot) ja niiden keskinäisvaikutuksista, joita voidaan luokitella, esimerkiksi kuuden kategorian alle: ihmiset, koneet, menetelmät, materiaalit, mittaukset ja ympäristö. Ja myös kaikki nämä vaihtelevat ajan yli.
Prosessin tutkiminen ajan suhteen on elintärkeää, jos olet kiinnostunut esimerkiksi:
- Prosessin nykyisestä suorituskyvystä
- Lähtötilanteen (baseline) määrittämisestä parannusta silmällä pitäen
- Parannustoimenpiteiden toimivuuden arvioinnista
- Tulevan suorituskyvyn arvioinnista
- Aikaansaatujen parannusten pysyvyydestä
Tätä ei oikeastaan voi ylikorostaa: Jos jätät prosessidatan luontaisen aikaelementin huomiomatta, saatat tehdä virheellisiä (tilastollisia) johtopäätöksiä. Erityissyyt ja satunnainen vaihtelu menevät sekaisin ja aiheutat vain lisää ongelmia (vaihtelua).
Lähteet:
- Deming, W. Edwards; Out of The Crisis; The MIT Press; Reissue ed (2018)
- Balestracci, Davis; Data Sanity; MGMA; 2nd Edition (2015)
- PERFECT- Menetelmäraportti; Terveyden ja hyvinvoinnin laitos (2009) (https://thl.fi/documents/10531/3549401/PERFECTMenetelmäraporttiV10.pdf vierailtu 22.5.2023)
Tutustu Minitab-kursseihin
Tilaa uutiskirje
Liity postituslistalle ja saat uusimmat artikkelit suoraan sähköpostiisi.
Tämä lomake on suojattu Google reCAPTCHA:lla. Lue tietosuojaseloste ja käyttöehdot.
Liittymällä postituslistalle hyväksyt Quality Knowhow Karjalainen Oy:n tietosuojaselosteen ja Quality Knowhow Karjalainen Oy voi lähettää sinulle ajankohtaisia artikkeleita, videoita sekä tietoa ja tarjouksia kursseista, kirjoista sekä ohjelmistoista.






Tämä lomake on suojattu Google reCAPTCHA:lla. Lue tietosuojaseloste ja käyttöehdot.