Johdanto
Teollisuudessa ja käytännössä vastaan tulevat datat ovat monesti monimutkaisia, moniulotteisia datoja. Tällaisten datojen käsittelyyn ja analysointiin voidaan soveltaa tilastomatemaattisia monimuuttujamenetelmiä. Nykyisenä tehokkaiden ja kehittyneiden tietokoneiden aikakautena tällaisten analyysien laskeminen ohjelmistojen avulla on varsin helppoa.
Tässä artikkelissa tarkoituksena on esitellä yhden tilastomatemaattisen monimuuttujamenetelmän, pääkomponenttianalyysin (Principal Component Analysis = PCA) laskentaa Minitab-ohjelmiston avulla. Tämä artikkeli ei ole teoreettinen esitys kyseisestä analyysimenetelmästä. Teoreettinen esitys menetelmästä löytyy esimerkiksi Johnsonin ja Wichernin kirjasta/1/, Rencherin kirjasta/2/ sekä Hair et al./3/ kirjoittamasta kirjasta.
Tilastolliset monimuuttujamenetelmät
Tilastollisia monimuuttujamenetelmiä on olemassa monia erilaisia. Tilastollisia monimuuttujamenetelmiä ovat esimerkiksi: moniulotteinen lineaarinen regressio (Multivariate Linear Regression), pääkomponenttianalyysi (Principal Component Analysis = PCA), faktorianalyysi (Factor Analysis = FA), kanoninen korrelaatio (Canonical Correlation Analysis = CCA), diskriminantti- eli erotteluanalyysi (Discriminant Analysis), klusteri- eli ryhmittelyanalyysi (ClusterAnalysis = CA), moniulotteinen skaalaus (Multidimensional Scaling = MDS), moniulotteinen varianssianalyysi (Multivariate Analysis of Variance = MANOVA) ja korrespondenssianalyysi (Correspondence Analysis = CA)./1//2/
Tilastomatemaattisten monimuuttujamenetelmien ominaisuuksia voidaan kuvata seuraavan luettelon mukaisesti/1/.
- Datan pienennys ja rakenteen yksinkertaistaminen
Tutkittu ilmiö on esitetty niin yksinkertaisesti kuin mahdollista, uhraamatta yhtään arvokasta informaatiota. Toiveena on, että tämä tekee tulkinnan helpommaksi.
- Lajittelu ja ryhmittely
Luodaan ryhmiä, joissa on keskenään samankaltaisia objekteja tai muuttujia, joiden ryhmittely perustuu mitattuihin ominaisuuksiin. Vaihtoehtoisesti voidaan tarvita sääntöjä, joiden avulla ryhmittely voidaan suorittaa.
- Muuttujien välisen riippuvuusrakenteen tutkiminen
Tutkitaan ovatko muuttujat riippumattomia, vai onko niiden välillä jonkinlainen riippuvuusrakenne. Jos muuttujien välillä on riippuvuusrakenne – millainen rakenne on.
- Ennustaminen
Muuttujien välisten riippuvuusrakenteen tutkiminen. Tavoitteena on se, että yhden tai useamman muuttujan arvoja voidaan ennustaa muiden muuttujien havaintojen perusteella.
- Hypoteesin muodostaminen ja testaaminen
Täsmälliset tilastolliset hypoteesit on muodostettu niin, että moniulotteisten populaatioiden parametreja on testattu. Tavoitteena voi olla esimerkiksi aikaisempien käsitysten vahvistaminen.
Pääkomponenttianalyysistä
Pääkomponenttianalyysin esitteli vuoden 1901 artikkelissaan Karl Pearson/4/. Edelleen menetelmää kehitti Harold Hotelling, joka esitteli tutkimuksensa kahdessa julkaisussa vuonna 1933./5//6/
Tässä artikkelissa pääkomponenttianalyysin idea esitetään yksinkertaistettuna. Tarkoituksena on esitellä pääkomponenttianalyysin laskeminen Minitab-ohjelmistolla. Pääkomponenttianalyysin tarkoituksena on esittää alkuperäisen aineiston muuttujat uusina muuttujina. Nämä uudet muuttujat ovat keskenään korreloimattomia (ortogonaalisia) ja ne ovat alkuperäisten muuttujien lineaarisia kombinaatiota. Pääkomponenttianalyysin ajatus on yksinkertaistettuna seuraavassa kaavassa (Kaava 1).

Pääkomponenttianalyysi Minitabilla
Aineiston kuvaus
Pankin lainaosasto on kerännyt dataa lainanhakijoista. Kyseisessä aineistossa on kahdeksan sosioekonomista ominaisuutta kuvaavaa muuttujaa, joissa kussakin on 30 havaintoa, tarkempi aineiston kuvaus on seuraavassa taulukossa (Taulukko 1).

Pääkomponenttianalyysi
Aineiston analysointi on esitetty artikkelin lopussa olevassa Youtube-videossa. Tässä on raportoitu analysoinnin tulokset ja niiden tulkinnat. Analysointi on aloitettu laskemalla yhtä monta pääkomponenttia, kuin aineistossa on muuttujia. Tämän avulla pyritään pääkomponenttien määrää vähentämään, jotta päädytään lopulliseen ratkaisuun. Jolliffe/7/ on esitellyt monia sääntöjä, joiden avulla voi määrittää tarvittavien pääkomponenttien lukumäärän. Kuvassa 3 on analyysitulokset aineistolle, jolle on laskettu 8 pääkomponenttia.

Kuvasta 3 nähdään, että ensimmäinen pääkomponentti selittää 44,3 % tutkittavan aineiston hajonnasta ja toinen pääkomponentti selittää 26,6 % tutkittavan aineiston hajonnasta. Kumulatiivisesti kaksi ensimmäistä pääkomponenttia selittävät 71 % aineiston hajonnasta ja vastaavasti viisi ensimmäistä selittävät 95,8 %. Sama informaatio näkyy myös Scree Plotista (Kuva 4).
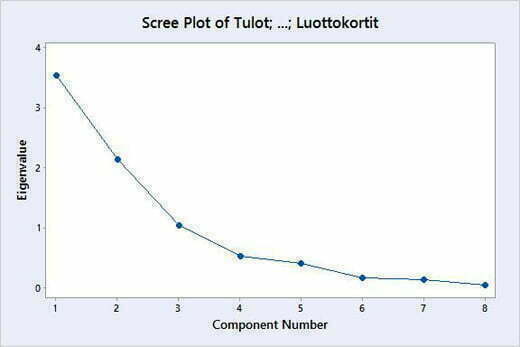
Katsottaessa kuvaa 3 ja kuvaa 4 voidaan määritellä tarvittavien pääkomponenttien lukumäärä. Tähän on olemassa monia eri sääntöjä/7/. Kuvasta 3 nähdään, että kolme ensimmäistä pääkomponenttia selittävät 84,1 % (>80 %) aineiston hajonnasta. Vastaavasti Scree Plotissa kuvaaja on lähes suora pääkomponentin 3 jälkeen, eli pääkomponenttien määrän lisääminen 4…8 ei paranna aineiston hajonnan selitystä.
Lopullinen pääkomponenttianalyysi on laskettu käyttäen kolmea pääkomponenttia. Kyseiset analyysit on edelleen esitetty artikkelin lopussa olevassa Youtube-videossa. Analyysitulokset ovat tulkintoineen seuraavissa kuvissa (Kuva 5 – Kuva 11).


Kuva 5 on sama, kuin aikaisemmin esitetty kuva 3. Minitab tekee tämän analyysin osan niin, että se laskee yhtä monta pääkomponenttia, kuin aineistossa on muuttujia. Samoin myös kuva 6 on sama, kuin kuva 4. Näiden kuvien perusteella päädytään edelleen siihen, että kolme pääkomponenttia on riittävä määrä.
Pääkomponenteille saadaan tulkinnat tutkimalla niiden latauksia. Tutkittavan aineiston lataukset kolmelle pääkomponentille nähdään kuvasta 7 ja kahdelle ensimmäiselle pääkomponentille kuvasta 8.
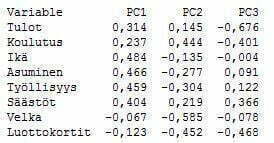
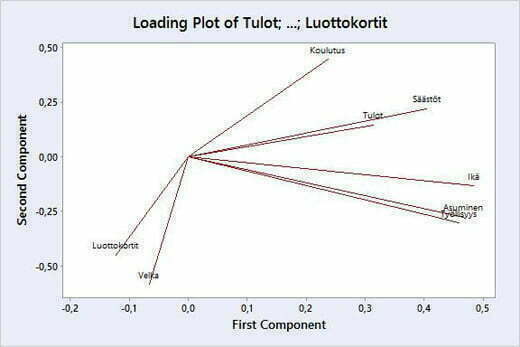
Kuvasta 7 ja 8 huomataan, että itseisarvoltaan suurimmat lataukset pääkomponentilla 1 on muuttujilla: Ikä, Asuminen, Työllisyys ja Säästöt. Kyseisen pääkomponentin tulkinta voisikin olla hakijan taustatiedot. Itseisarvoltaan suurimmat lataukset pääkomponentilla 2 on muuttujilla: Velka ja Luottokortit. Tulkinta voisi olla luottohistoria. Pääkomponentille 3 latautuvat muuttujat: Tulot ja Koulutus.Tulkinta voisikin olla akateeminen- ja tuloluokitus.
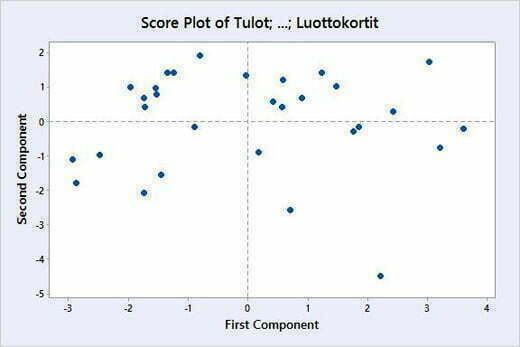
Score Plotista (Kuva 9) nähdään, miten aineiston havainnot sijaitsevat kahdella ensimmäisellä pääkomponentilla. Tätä kuvaa voidaan käyttää, kun halutaan tarkastella, onko tutkittavassa datassa esimerkiksi trendejä tai outliereita. Tässä kuvassa oikeassa alanurkassa oleva havainto voi olla outlieri, joten sitä pitää tutkia lisää.
Score Plotista (Kuva 9) nähdään, miten havainnot sijoittuvan kahdelle ensimmäiselle pääkomponentille ja Biplotissa (Kuva 10) on yhdistetty latauskuvan (Kuva 7) ja Score Plotin (Kuva 9) tiedot.
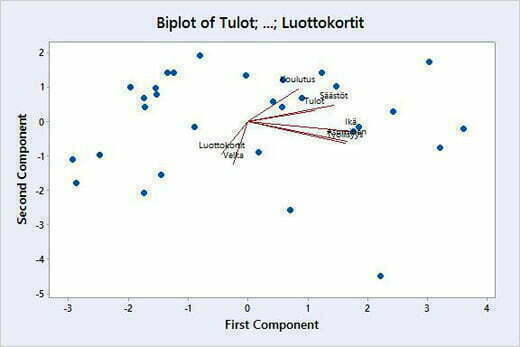
Kuvassa 10 on Biplotissa esitetty graafisesti kahden ensimmäisen pääkomponentin lataukset sekä aineiston havaintojen sijainti niillä. Biplotissa on siis yhdistetty kuvan
Minitabilla voidaan laskea Outlier Plot. Tämän kuvaajan avulla voi tutkia, onko analyysi ok, vai onko siinä outliereita. Lainanhakija datan pääkomponenttianalyysin Outlier Plot on seuraavassa kuvassa (Kuva 11).


Mahalanobisin etäisyyden perusteella Minitab laskee referenssiarvon, johon havaintoja verrataan. Jos havainto on suurempi kuin referenssiarvo, se on outlieri ja analyysissa on ongelmia. Kuvassa 12, kaikki arvot ovat referenssiviivan alapuolella, joten siinä ei ole outlierieta eikä analyysissä ole ongelmia.
Johtopäätökset ja yhteenveto
Tässä artikkelissa on esitetty pääkomponenttianalyysin laskenta Minitab-ohjelmistolla. Tarkoituksena ei ollut kirjoittaa teoreettista kuvausta kyseisestä tilastomatemaattisesta menetelmästä. Tavoitteena oli esimerkin avulla pyrkiä kuvaamaan kyseisen menetelmän laskennan helppoutta Minitabilla sekä menetelmän tehokkuutta.
Tämän artikkelin esimerkissä saatiin monen muuttujan aineisto tiivistettyä kolmelle pääkomponentille, jotka yhdessä kuvasivat yli 80 % alkuperäisen aineiston hajonnasta.
Lähteet:
- Johnson, R. A. & Wichern, D. W., 2002. Applied Multivariate Statistical Analysis. 5th edition. Prentice Hall.
- Rencer, A. C. 2002. Methods of Multivariate Analysis. 2nd edition. John Wiley & Sons, Inc.
- Hair, J. F., Anderson, R. E., Tatham, R. L. & Black, W. C., 1998. Multivariate Data Analysis. Prentice Hall.
- Pearson, K., 1901. On Lines and Planes of Closest Fit to Systems of Points in Space. Philosophical Magazine, 2, pp. 559-572
- Hotelling, H., 1933a. Analysis of a Complex of Statistical Variables into Principal Components. Journal of Educational Psychology, 24(6), pp. 417-441.
- Hotelling, H., 1933b. Analysis of a Complex of Statistical Variables into Principal Components. Journal of Educational Psychology, 24(7), pp. 498-520
- Jolliffe, I. T., 1986. Principal component analysis. Springer-Verlag
- Mahalanobis, P. C., 1936. On the Generalized Distance in Statistics. Proceedings of the National Institute of Sciences of India, 2(1), pp. 49-55.
Tilaa uutiskirje
Liity postituslistalle ja saat uusimmat artikkelit suoraan sähköpostiisi.
Tämä lomake on suojattu Google reCAPTCHA:lla. Lue tietosuojaseloste ja käyttöehdot.
Liittymällä postituslistalle hyväksyt Quality Knowhow Karjalainen Oy:n tietosuojaselosteen ja Quality Knowhow Karjalainen Oy voi lähettää sinulle ajankohtaisia artikkeleita, videoita sekä tietoa ja tarjouksia kursseista, kirjoista sekä ohjelmistoista.

Tämä lomake on suojattu Google reCAPTCHA:lla. Lue tietosuojaseloste ja käyttöehdot.