Numeroihin voidaan suhtautua monella tapaa. Yleisesti numeroita pidetään kätevinä, mitä tulee määrien tai asioiden suuruuden arviointiin. Dataa ja erilaisia lukuja on keskimääräisessä yrityksessä nykyään käytössä jopa liialti. Useiden mittaristojen monimutkaisuuden yhteensovittamiseksi on pyritty visualisoimaan luvut palkeiksi, väreiksi tai indekseiksi. Nämä ovat aiheita, joita ei tässä artikkelissa käsitellä, mutta kuuluvat yleisen ”numeroiden lukutaidon” ja ”tilastollisen ajattelun” tarpeiden alle. Hyvin yleinen suhtautuminen lukuihin ja dataan on, että kahden erilaisen luvun taustalla täytyy olla jonkinlainen syy tai jos luvut eivät ole samat, niin ne ovat eri. Koska maailmassa on epämääräisyyttä, olisi hyvä ymmärtää tilastollista ajattelua ja myös siinä käytettäviä tekniikoita.
Hypoteesitestit ja luottamusvälit
Vaikka tilastollisten termien ja menetelmien perusteet olisivat tuttuja, on oppikirjojen tai yliopistokurssien esimerkeistä joskus vaikea siirtyä soveltamiseen oikeassa elämässä. Kannattaa silti yrittää, sillä testit ja hyvin suunniteltu näytteenotto säästävät yleensä aikaa ja rahaa!
Koska kaikki maksaa, haluaisimme tehdä riittävän hyviä päätöksiä mahdollisimman pienillä kustannuksilla. Tilastollisten menetelmien hienous on päätösten tekemisen osittaisesta tiedosta, ei tarvita kaikkea dataa ymmärtääksemme jotain. Tilastollisten testien ja menetelmien käyttö perustuu pitkälti näytteen ottamisen ajatukseen, jota on esitetty kuvassa 1.
Valitusta populaatiosta (perusjoukosta) otetaan tutkittavan kysymyksen perusteella näyte, josta tehdyn yhteenvedon perusteella vastataan esitettyyn kysymykseen ja tehdään päätelmä itse populaatiosta.
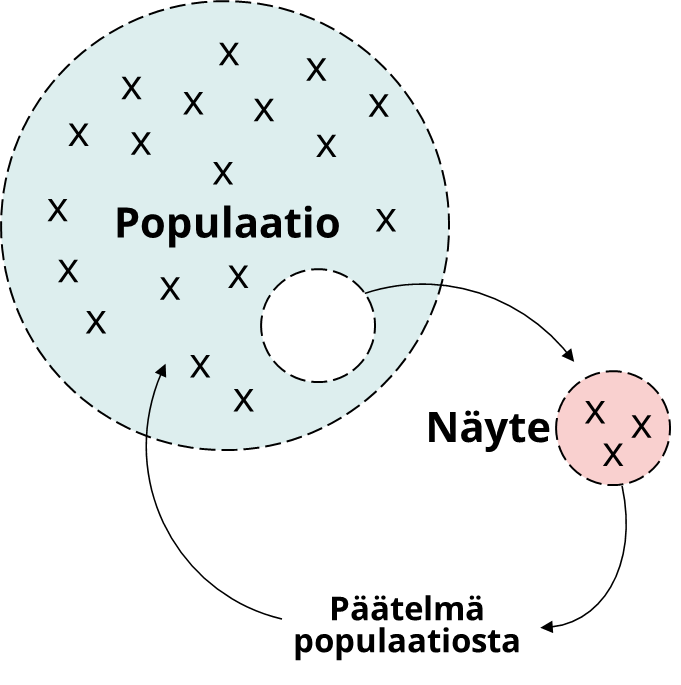
Toisin sanoen, populaatiosta otettua näytettä käytetään tekemään johtopäätös tai päätelmä jostain kiinnostavasta populaation ominaisuudesta, kuten ihmisten pituudesta, tuotteiden lujuudesta, palveluiden jonotusajasta tai mistä hyvänsä. Tähän menettelytapaan liittyy aina epävarmuus, joten halutusta parametrista saadaan aina vain arvio.
Esimerkiksi arvioitaessa populaation keskiarvoa, tämä epävarmuus nähdään luottamusvälissä. Tyypillinen 95% luottamusväli kertoo, että populaation keskiarvo (tai muu tunnusluku) on 95 kertaa 100:sta ilmoitetulla välillä. Mitä pienempi näyte ja mitä suurempi on näytteen sisäinen hajonta, sitä suuremmaksi populaation luottamusväli muodostuu. Luottamusväli kertoo siis alueen, jonka sisällä tutkittavan parametrin, kuten populaation keskiarvo on tietyllä todennäköisyydellä. Tulee muistaa, että luottamusväli ei ennusta mille alueelle yksittäiset havainnot sijoittuvat.
Oma virheensä näytteestä vedettäviin johtopäätöksiin tulee edustavuudesta, eli siitä onko näytteeseen valittu populaatiota aidosti edustava joukko havaintoja. Jos näin ei ole, tulee saataviin tuloksiin vinouma (bias). Tämän mahdollisuutta pyritään yleensä pienentämään tekemällä näytteenotannasta mahdollisuuksien rajoissa mahdollisimman satunnaista.
Toinen käyttötarkoitus tilastollisille menetelmille on vertailu ja hypoteesitestaus. Eli voimmeko todeta eri populaatioiden olevan toisistaan poikkeavia, eroavan jostain vertailuarvosta, olevan erilaisia tai toistensa kaltaisia. Näissä käytämme varsinaisia hypoteesitestejä. Hyvä listaus hypoteesitesteistä löytyy esimerkiksi Minitab 21 -ohjelmiston Assistant valikosta (Assistant> Hypothesis test) (kuva 2).
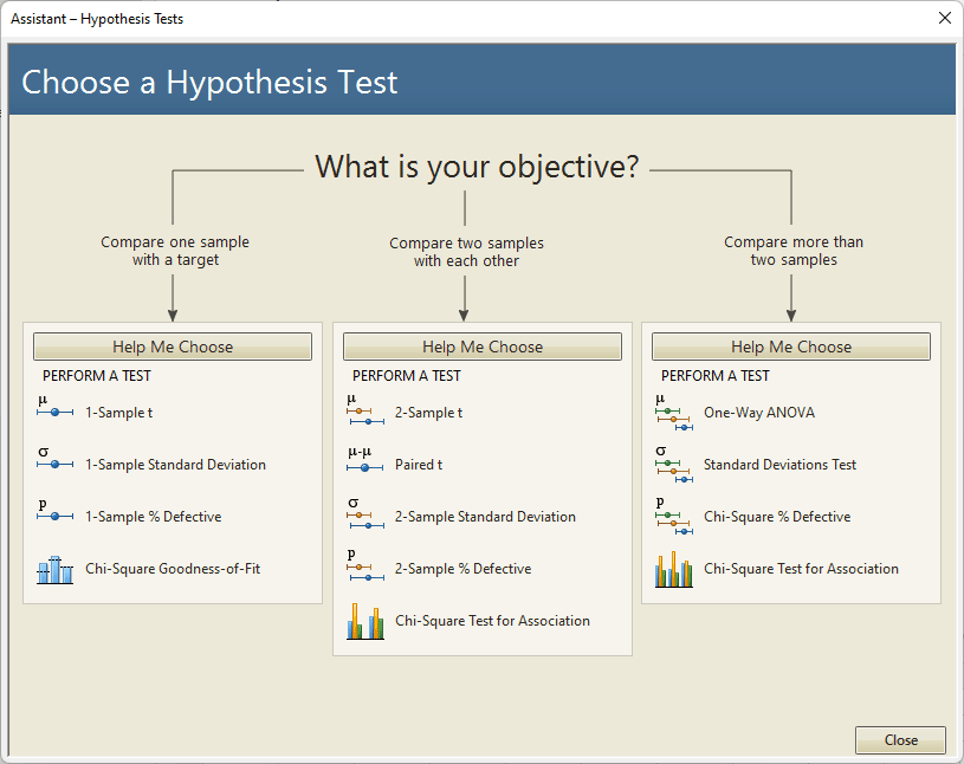
Valikosta löytyy perustestit, jotka laatuinsinöörin, päällikön tai esimerkiksi liiketoiminnan kehittäjän tai kenen tahansa numeroiden, epävarmuuksien ja päätösten parissa työskentelevän tulisi hallita.
Hypoteesitestien idea on ymmärtää, onko olemassa muutosta, joka on suurempi kuin satunnainen muutos. Tai vastaavasti todeta, että muutosta ei ole tapahtunut. Tätä kutsutaan tilastolliseksi merkittävyydeksi, eli voidaanko havaita muutos, joka on suurempi kuin voisi olettaa tapahtuvan sattumalta.
Tilastollinen merkittävyys tulee aina pitää erillään käytännön kannalta merkittävästä, sillä vaikka löytäisimme tilastollisesti merkittävän eron, ei se tarkoita, että sillä olisi mitään käytännön merkitystä. Tilastollisesti merkittävä kuulostaa aina hienolta, mutta ei välttämättä tarkoita uutta merkittävää tietoa. Toki on myös paljon tilanteita, jotka eivät tarvitse tilastollista analyysiä. Kun muutos on niin ilmeinen, että se voidaan havaita jo näytteiden visuaalisesta arvioinnista (esim. boxplot-kuvaajat), ei hypoteesitesti p-arvoineen tuo paljoakaan lisäarvoa.
Yksinkertaisimmat testit, josta tilastollisten menetelmien oppikirjat tai koulutukset lähtevät liikkeelle ovat yhden ja kahden riippumattoman otoksen testit, Minitabissa 1-Sample t ja 2-sample t. Näissä testeissä näytteiden olevan toisistaan riippumattomia. Yhden otoksen testillä (1-sample t) voidaan verrata näytettä vertailuarvoon ja siten arvioida onko populaatio suurempi, pienempi tai erisuuri verrattuna vertailtavaan arvoon. Sinänsä kaikkien hypoteesitestien idea on samankaltainen, vaikkakin yksityiskohdat ja vaatimukset vaihtelevat.
Hypoteesitestien idean on nimensä mukaan tehdä päätös kahdesta vastakkaisesta hypoteesista. Nollahypoteesi (H0) olettaa että mikään ei ole muuttunut ja vaihtoehtoinen hypoteesi (H1), joka tulee voimaan jos nollahypoteesi kumotaan. Perusajatuksena on, että maailmassa kaikki on aina samanlaista ja tulee löytää näyttöä erosta. Jos todetaan että havaittu ero on suurempaa kuin satunnainen, voidaan vaihtoehtoinen hypoteesi ottaa käyttöön. Tässä päätöksessä tarkastellaan todennäköisyyslukua tai p-arvoa. Riippuen hyväksyttävästä riskistä, nollahypoteesi kumotaan kun p-arvo alle 0,1-0,05. Päätös käytettävästä riskistä tehdään ennalta, mutta emme mene siihen tässä enempää.
Hypoteesitestit voidaan tehdä myös manuaalisesti kun lasketaan tarvittavat parametrit ja sovelletaan tilastollisia taulukoita. Suositan menettelystä kiinnostuneita tutustumaan esimerkiksi teokseen General statistics (Warren, Brown, 1999). Seuraavaksi katsomme miten testit saadaan tehtyä Minitab 21 ohjelmalla.
Esimerkki: Suomalaisten suurten yritysten liikevaihdon kasvun arviointi näytteen avulla
Arvioidaan suurten suomalaisten yritysten liikevaihdon muutosta näytteen avulla. Talouselämä lehden (10.6.2022) top 500 listaus vuodelta 2022 esittää joukon erilaisia tunnuslukuja 500 suurimmasta suomalaisesta yrityksestä. Tästä saatavilla olevasta datasta laiska ekonomi haluaa saada arvion keskimääräisestä liikevaihdon muutoksesta ja nettotuloksesta. Koska pääsyä koko dataan ei ole, otetaan lehden listauksesta satunnainen 15 yrityksen näyte. Satunnaisiksi riveiksi (yrityksiksi) päätyivät seuraavat sijanumerot: 183, 244, 19, 422, 433, 257, 332, 203, 316, 476, 370, 314, 335, 47, 410.
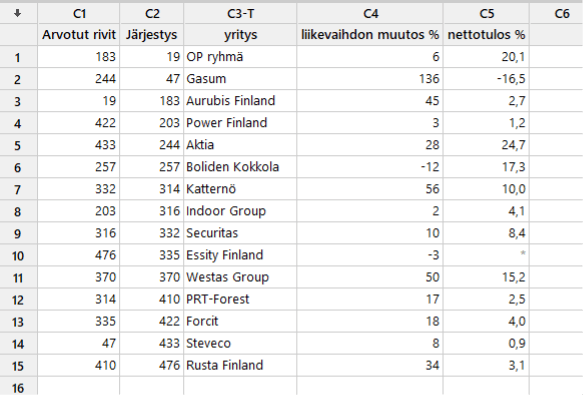
Minitabissa keskiarvon luottamusvälit populaatiolle saadaan esimerkiksi 1-sample t -testin valikosta tai graafisesta yhteenvedosta (Stat> Basic Statistics> Graphical summary). Tehdään ensiksi mainitun kautta ja valitaan Stat>Basic Statistics> 1-Sample t ja täytetään dialogi omalla datalla (kuva 4).
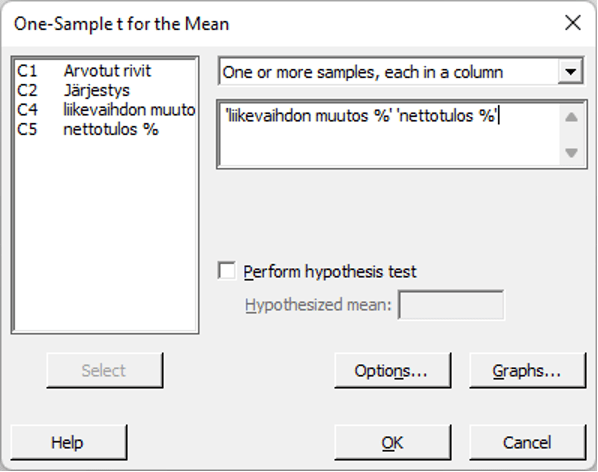
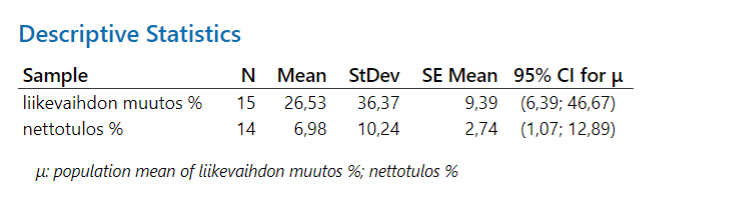
Kuvassa 5 (yllä) on esitetty Minitabin antamat kuvaavat statistiikat näytteistä ja 95% luottamusvälit populaation keskiarvolle (µ, myy). Tällä näytteellä saadaan arvio, että suomalaisten suurten yritysten keskimääräinen liikevaihdon muutos-% on ollut vuonna 2021-2022 välillä 6,39- 46,67 %. Vastaavasti nettotulos-% keskiarvo on välillä 1,07-12,89 %.
Mitä merkitystä tuloksella on? No ainakin molemmat ovat positiivisen puolella ja saimme arvion hakkaamatta kaikkea dataa tietokoneeseen. Voisimme olla myös kiinnostuneita testaamaan onko liikevaihdon muutos suurempaa kuin jonkinasteinen inflaation vauhti, sanotaan nyt vaikka 5%. Koska näyte on tilastollisesti pieni (alle 30) hypoteesitestiä suorittaessa tulisi varmistua näytteen normaalisuudesta. Epäsatunnaisesti jakautuneella näytteellä ja poikkeavilla arvoilla voi olla suuri vaikutus testin tuloksiin. Toki joskus vinouma on ihan tavallista.
Normaalisuuden testi löytyy Minitabissa valikosta Stat> Basic Statistics> Normality Test. Kuva testin ulostulosta (normaalisuuskuvaaja) esitetty kuvassa 6.
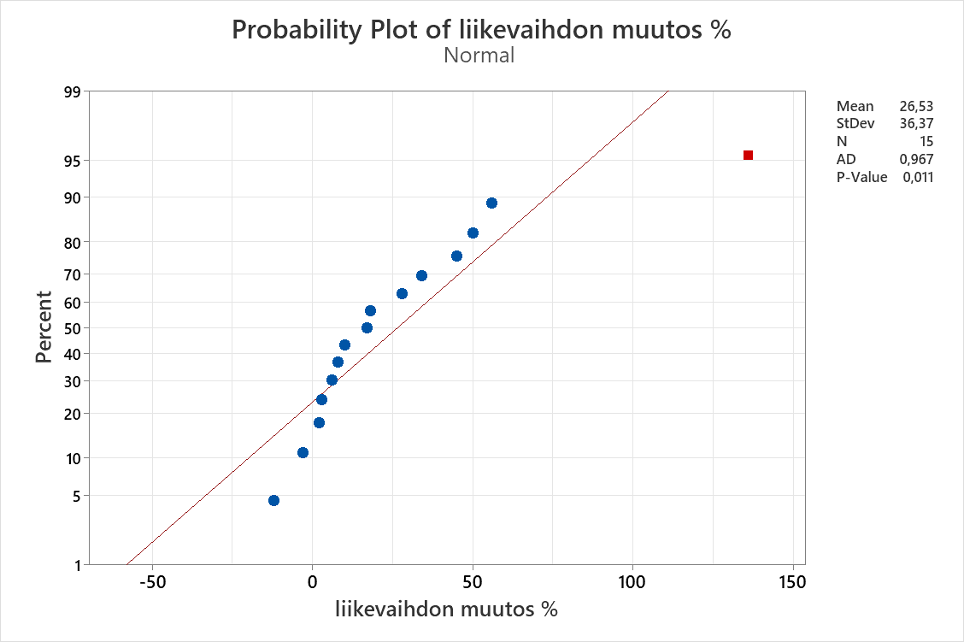
Kuvasta voidaan päätellä, että yksi havainnoista poikkeaa merkittävästi muista (punainen neliö). Tämä on Gasum, jonka liikevaihdon kasvu on ollut 136 %. Näytteen kerääjän tietojen perusteella tämä ei ole virheellinen tieto tai näppäilyvirhe, joten havainto jätetään näytteeseen. Voisi olla turvallisempaa kerätä suurempi näyte, mutta nyt siihen ei ole varaa.
Hypoteesitesti suoritetaan tässä tapauksessa yksisuuntaisena. Nollahypoteesi on, että populaation keskiarvo (myy, µ) on yhtä suuri 5% kanssa, ja vaihtoehtoinen että populaation keskiarvo (myy, µ) on suurempi kuin 5%.
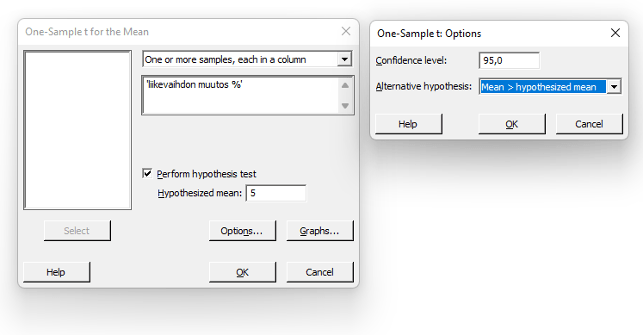
Kuvassa 7 (yllä) on näytetty yksisuuntaisen 1-sample t testin valinnat. Kuvassa 8 (alla) on esitetty testin tulokset, joista nähdään näytteen kuvaava statistiikka ja alempi luottamusväli populaation keskiarvolle (myy, µ). Testin hypoteesit esitetty muistutuksena ja koska P-arvo on alle sovitun riskitason (0,05) toteaisimme, että suomalaisten suurten yritysten liikevaihto on ollut suurempi kuin 5%.

Edellä esitetty esimerkki on yksinkertainen sovellutus hypoteesitestistä, jossa yritetään puutteellisella tiedolla ymmärtää tuntematonta populaatiota. Esitellyllä testillä on lukuisia sovelluksia ja kaikilla muilla vielä enemmän. Ideana olisi kuitenkin ymmärtää idea, jotta voi miettiä soveltamisen. Yleensä soveltaminen on aina teoriaa vaikeampaa!
Suosittelen hypoteesitestien perusteisiin tutustumista ja myös Minitabin Assistantin kokeilua kaikille numeroiden kanssa päätöksiä tekeville. Assistant sisältää hyvät neuvot ja ohjeet, sekä yksinkertaiset tulkinnat testin tuloksista, joilla pääsee helposti alkuun ja tilastollisen päätöksenteon jännään maailmaan!
Luettavaa:
Tilaa uutiskirje
Liity postituslistalle ja saat uusimmat artikkelit suoraan sähköpostiisi.
Tämä lomake on suojattu Google reCAPTCHA:lla. Lue tietosuojaseloste ja käyttöehdot.
Liittymällä postituslistalle hyväksyt Quality Knowhow Karjalainen Oy:n tietosuojaselosteen ja Quality Knowhow Karjalainen Oy voi lähettää sinulle ajankohtaisia artikkeleita, videoita sekä tietoa ja tarjouksia kursseista, kirjoista sekä ohjelmistoista.

Tämä lomake on suojattu Google reCAPTCHA:lla. Lue tietosuojaseloste ja käyttöehdot.