Data teollisuudessa
Erilaisen datan määrä teollisuudessa kasvaa nopeasti. Erilaisia asioita, kuten lämpötilaa, painetta jne. voidaan helposti mitata teollisuuden prosessien vaiheista. Vastaavasti datapankkien varastointikapasiteetit kasvavat nopeasti. Samoin tietokoneiden laskentatehot lisääntyvät nopeasti ja erilaiset matematiikka- ja tilastomatematiikkaohjelmistot ovat tulleet kaikkien saataville. Näiden ohjelmistojen avulla pystytään laskemaan nopeasti monimutkaisia analyysejä ja data saadaan jalostettua tiedoksi, jonka avulla voidaan toimia. Yritysten pitääkin ymmärtää, että pelkän datan keruusta keruun itsensä vuoksi ei ole mitään tavoitteiden pitää aina olla pidemmällä tiedon luomisessa. Toisaalta tohtori W. Edwards Deming on tiivistänyt kuuluisassa lainauksessaan datan keräämisen tärkeyden.
”In God we trust; all others must bring data”
Dr. W. Edwards Deming
Tilastotiede
Amerikan tilastollinen yhdistys (American Statistical Association) määrittelee tilastotieteen ja tilastotieteilijät internetsivuillaan seuraavasti:
”Statistics is a science of collection, analysis, and presentation of data. Statisticians contribute toScientific enquiry by applying their knowledge to the design of surveys and experiments; thecollection, processing, and analysis of data ; and interpretation of results.”
Tilastotieteen ja tilastotieteilijöin määritelmän mukaan, tilastotiede on tieteenala, joka keskittyy datan keruuseen ja datan esittämiseen. Vastaavasti tilastotieteilijät käyttävät osaamistaan datan keruuseen (erilaiset kyselyt ja kokeet) sekä datan analysointiin ja tulosten tulkintaan.
Tilastotieteessä mainitaan yleensä olevan kaksi (joskus kolme) lähestymistapaa, Frekventistinen tilastotiede ja Bayesiläien tilastotiede (Barnett, 1982).
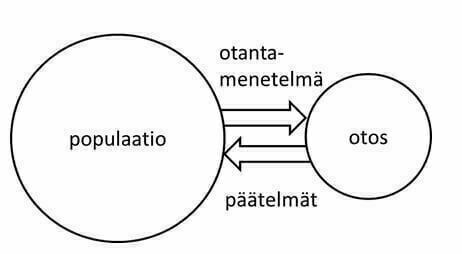
Seuraavassa on kerrottu kahdesta yleisimmästä. Frekventistinen tilastotiede perustuu Sir R. A. Fisherin, E. S. Pearsonin ja J. Neymanin työhön. Frekventistinen tilastotiede perustuu näytedataan, josta tehtävien analyysien perusteella tehdään päätelmiä koko populaatiosta. (Barnett, 1982; Cox, 2006) Frekventistisessä saadun näytteen pohjalta muodostetaan kuvitteellisia näytteitä ja tutkitaan mitatun näytteen sijoittumista tuohon joukkoon. Tästä saadaan laskettua havaittu merkitsevyystaso (p-arvo), ei oikeaa todennäköisyyttä. Toisen lähestymistavan, Bayesiläisen tilastotieteen ajatus perustuu rovasti Thomas Bayesin 1763 julkaisemaan artikkeliin. Bayesiläisessä tilastotieteessä lasketaan millä todennäköisyydellä eri alkuehdot tuottavat mitatun datan ja tämä kerrotaan priori-informaatiolla, jos sellaista on saatavilla.
Davenport ja Krusak (2000) esittävät viisi eri menetelmää siihen, miten data voidaan muuntaa informaatioksi. Nämä menetelmät ovat:
- Analysoimalla
- Dataa voidaan analysoida matemaattisesti tai tilastomatemaattisesti
- Kategorisoimalla
- Tietämällä datan yksiköt ja komponentit
- Tiivistämällä
- Data voidaan tiivistää tiiviimpään muotoon
- Kontekstualisoimalla
- Mihin tarkoitukseen data on kerätty
- Korjaamalla
- Poistamalla datasta virheet
Davenportin ja Krusakin (2000) listan ensimmäinen kohta on tämän kirjoituksen kannalta mielenkiintoinen. Data voidaan siis muuntaa tiedoksi analysoimalla.
Oikeiden tilastomatemaattisten ja matemaattisten analyysien laskenta vaatii yritykseltä satsauksia. Yritysten pitää palkata asiantuntijoita, jotka pystyvät nämä analysoinnit suorittamaan. Yritysten pitää tarjota heille tarvittavat työvälineet analyysien suorittamiseksi. Näin yritys varmistaa sen, että dataa ei enää kerätä vain keräämisen itsensä vuoksi. Data saadaan jalostettua tiedoksi jonka perusteella yrityksen toimintaa voidaan ohjata ja varmistaa sen pärjääminen markkinoilla.
Erilainen data ja sen analysointi
Psykologi S. S. Stevens esitti vuonna 1946 julkaistussa artikkelissaan kuuluisan mittausdatan luokittelun. Stevensin (1946) data voitiin luokitella kuvan 1 mukaisesti neljään eri luokkaan.

Stevensin (1946) luokittelussa mittausdatan luokat olivat: nominaaliasteikollinen, ordinaaliasteikollinen, intervalliasteikollinen ja suhde asteikollinen. Agrestin (2002 ja 2010) mukaan nominaaliasteikollisella datalla ei ole mitään luonnollista järjestystä se voi olla esimerkiksi henkilön mielimusiikkityyli (klassinen, jazz tai rock). Vastaavasti mittausdataa, jossa on järjestyneet kategoriat kutsutaan ordinaaliasteikolliseksi dataksi, esimerkiksi potilaan kunto (hyvä, ok, huono tai kriittinen). (Agresti, 2002; Stevens 1946) Tyypillinen esimerkki intervalliasteikollisesta datasta on lämpötila mitattuna Celsiusasteina ja Fahrenheitteina, molemmissa näissä lämpötilasteikoissa ei ole absoluuttista nollaa. (Stevens, 1946; Siegel, 1957; Khurshid & Sahai, 1993) Vastaavasti suhde asteikollisessa datassa on absoluuttinen nolla, esimerkiksi lämpötila Kelvin-asteikolla mitattuna.
Stevens (1946) myös esitti, että oikea tilastomatemaattinen analyysimenetelmä voidaan valita hänen mittausdatan luokitteluun perustuen. Myöhemmin monet tutkijat ovat kritisoineet Stevensin (1946) ajatuksia, esimerkiksi Lord (1953) esitti, että mittauksiin liittyvät asiat pitäisi ymmärtää itsenäisesti ilman tilastollisia näkemyksiä. Vastaavasti Velleman ja Wilkinson (1993) olivat sitä mieltä, että analyysimenetelmän valinta datan luokan perusteella ei onnistu, koska harvoin oikea data noudattaa datan luokittelun vaatimuksia. Khurshid ja Sahai (1993) tutkivat kirjoittajia, jotka olivat kritisoineet Stevensiä ja päätyivät tutkimuksessaan siihen, että oikea analyysimenetelmä pitää valita ennemmin jakauman perusteella, kuin Stevensin luokittelun perusteella.
Tilastotiede teollisuudessa ja sen haasteet
Kankaanranta (2012) on tutkimuksessaan selvittänyt kyselyn avulla määritellyt mitä teollisuustilastotiede (Industrial Statistics) on ja mitkä ovat kyseisen tieteenalan suurimmat haasteet tulevaisuudessa. Kyselyn perusteella teollisuustilastotiede on yksinkertaisesti teollisuudessa sovellettua tilastotiedettä. Toisaalta kyseisen tieteenalan tavoitteena on soveltaa tilastollista ajattelua niin, että yritys jossa työskennellään menestyisi.
Kankaanrannan (2012) tutkimuksen perusteella on myös tärkeää, että teollisuustilastotieteilijä ottaa johtavan roolin organisaation haasteellisissa asioissa ja työskentelee sen puolesta, että tilastolliset menetelmät ja ajatteluttavat otetaan käyttöön läpi koko organisaation.
Samoin Kankaanrannan (2012) mukaan teollisuustilastotieteen haasteita on se, että monet ihmiset, jotka osaavat käyttää jotakin tilastomatemaattista ohjelmistoa, kuvittelevat tällä perusteella pystyvänsä tekemään tilastollisesti oikeita päätöksiä. Samoin ongelmana on myös se, että monet ei-tilastotieteilijät eivät ymmärrä hajontaa ja sitä, miten se vaikuttaa heidän havaintoihinsa.
Yhteenveto
Koska datan määrä lisääntyy jatkuvasti teollisuudessa tarvitaan jatkuvasti entistä tehokkaampia menetelmiä tämän tiedon analysoimiseen. Tilastomatemaattiset menetelmät ovat erittäin tehokkaita tällaiseen tarkoitukseen. Samoin näitä menetelmiä osaavien asiantuntijoiden merkitys lisääntyy jatkossa huomattavasti teollisuudessa. Googlen pääekonomisti Hal Varian (2009) on ilmaissut asian seuraavasti:
”I keep saying that the sexy job in the next ten years will be statisticians.People think I´m joking, but who would quessed that computer engineersWould´ve been the sexy job of the 1990s.”
Edellä esitetyn perusteella voidaan siis helposti ajatella miksi yritysten pitäisi toiminnassaan lisätä tilastomatemaattisten menetelmien soveltamista ja työntekijöiden kouluttamista tämän alan asiantuntijoiksi. Koulutukseen tarjoaa hyviä mahdollisuuksia esimerkiksi monet eritasoiset Six Sigma -koulutukset. Lisäksi tilastotieteen teoriasta kiinnostuneille voi olla etua soveltuvin osin eri yliopistojen kurssien opiskelu.
Lähteet:
- Agresti, A., 2002. Categorical Data Analysis. Wiley-Interscience
- Agresti, A., 2010. Analysis of Ordinal Data. Wiley
- American Statistical Association (http://www.amstat.org/careers/whatisstatistics.cfm)
- Barnett, V., 1982. Comparative Statistical Inference. Chichester: John Wiley & Sons
- Cox, D.R., 2006. Principles of Statistical Inference. Cambridge: Cambridge University Press
- Davenport, T.H. & Prusak, L., 2000. Working Knowledge. Harward Business Review Press
- Devore, J.L., 2011. Probability and Statistics for Engineering and the Sciences. Cengage Learning
- Kankaanranta, J., 2012. Applications of Industrial Statistics. University of Turku
- Khurshid, A. & Sahai, H., 1993. Scales of Measurements: An Introduction and a Selected Bibliography. Quality and Quantity, 27, pp.303-324.
- Lord, F.M., 1953. On the Statistical Treatment of Football Numbers. American Psychologist, 8, pp.750-751.
- Siegel, S., 1957. Nonparametric Statistics. The American Statistician, 11(3), pp.13-19.
- Stevens, S.S., 1946. On the Theory of Scales of Measurement. Science, 103, pp.677-680
- Varian, H., 2009. The McKinsey Quaterly
- Velleman, P.F. & Wilkinson, L., 1993. Nominal, Ordinal, Interval and Ratio Typologies are Misleading. The American Statistician, 47(1), pp.65-72.
Tilaa uutiskirje
Liity postituslistalle ja saat uusimmat artikkelit suoraan sähköpostiisi.
Tämä lomake on suojattu Google reCAPTCHA:lla. Lue tietosuojaseloste ja käyttöehdot.
Liittymällä postituslistalle hyväksyt Quality Knowhow Karjalainen Oy:n tietosuojaselosteen ja Quality Knowhow Karjalainen Oy voi lähettää sinulle ajankohtaisia artikkeleita, videoita sekä tietoa ja tarjouksia kursseista, kirjoista sekä ohjelmistoista.
Tämä lomake on suojattu Google reCAPTCHA:lla. Lue tietosuojaseloste ja käyttöehdot.