Prosessin ja työkoneen säätäminen ja asettaminen – OSA III

Suorituskyvyn parantaminen

Ensimmäisessä^/6/ ja toisessa^/7/ artikkelissa käsiteltiin prosessin keskiarvon säätämistä eli asetusta – kuinka prosessin keskiarvo asetetaan ”riittävän” lähelle ideaalista nominaalia. Lisäksi oletettiin, että tiedossa on säätö”nuppi”, tekijä tai tekijät, jolla prosessin keskiarvoa työntekijä voi muuttaa. Autossa ohjauspyörä, kaasu, jarru jne.

Säätö, asetus, voi tapahtua kolmella tavalla;

1. Tässä kolmannessa artikkelissa käsitellään tilannetta, jossa ei ole tunnettua selkeää säätävää/ohjaavaa tekijää tai tekijöitä on lukuisia, joiden avulla prosessia ”säädetään”. Tyypillisesti tilanne esiintyy palveluprosesseissa ja monimutkaisissa tuotantoprosesseissa, joiden tuotteet edustavat korkeaa teknologista tasoa. ”Asentajakoe” mahdollistaa nopean ja tehokkaan tavan. Säädön sijaan käytetään usein termiä prosessin kyvykkyys ja sen parantaminen. Six Sigma tai Lean Six Sigma edustavat menetelmiä, joilla asetus ja säätö voidaan toteuttaa tai vaihtoehtoisesti suorituskykyä voidaan nostaa.
   
2. Yksi tunnettu säätötekijä: Keräämällä riittävän suuri näyte n (kpl) ”kerralla” ja määrittämällä tästä keskiarvo. Jos keskiarvo poikkeaa kriittisestä arvosta nominaali ± Δσ (taulukko osa I^/6/), tehdään säätö. Jos keskiarvo oli kriittisen ”haarukan T± Δσ sisällä, säätöä ei tehdä. Jos säätö joudutaan tekemään (arvo ulkona haarukasta), kerätään säädön jälkeen uusi n (kpl) suuruinen näyte niin kauan, kunnes säätöä ei tarvitse suorittaa. Kun tämä tila saavutetaan, prosessin keskiarvo on nominaali T ±2Δσ sisällä n. 98% todennäköisyydellä ja siirrytään prosessin ohjaukseen. Kysymys on keskiarvon näytepoikkeaman testauksesta nominaalia T vasten eli hypoteesitestistä.
   
3. Sekvenssisäätö: Toisessa ns. sekvenssisäädössä prosessista otetaan ”sopivin välein” yksi näyte esimerkiksi kerran vuorossa ja näistä näytteistä lasketaan kumulatiivista n suuruista keskiaroa (liukuvaa keskiarvoa) ja jos tämä keskiarvo ylittää kriittisen arvon nominaali T ± Δσ (taulukko osa II), suoritetaan säätö ja aloitetaan uusi kumulatiivisen keskiarvon kerääminen. Näytteitä kerätään niin kauan, kunnes koko edeltä käsin määritetty sekvenssi saadaan toteutettua. Kun tämä saavutetaan, prosessin keskiarvo on nominaali T ±2Δσ sisällä n. 97 % todennäköisyydellä. Tällöin vaadittu prosessin keskiarvo on saavutettu ja siirrytään prosessin ohjaukseen.

Prosessin ideaalitila muodostuu neljästä ehdosta – stabiilisuus, operatiivinen yhdenmukaisuus, keskiarvon asettaminen ja prosessin kyvykkyys:

1. Prosessi on oltava luontaisesti kyvykäs yhdenmukaisiin tuloksiin. Toisin sanoen prosessin on oltava stabiili yli ajan.
   
2. Valmistajan on toimittava prosessissa stabiilisti ja yhdenmukaisella tavalla. Operaation – prosessin tai koneen – olosuhteita ei voi valita tai muuttaa mielivaltaisesti.
   
3. Prosessin keskiarvo on asetettava ja ylläpidettävä sopivalla tasolla.
   
4. Prosessin luonnolliset toleranssit on oltava pienemmät kuin tuotteen/palvelun spesifioidut toleranssit (suunnitteluvaatimus).

Prosessin kyvykkyys

Oletetaan, että ehdot 1, 2 ja 3 ovat toteutuneet ainakin kohtuullisessa määrin. Prosessi on stabiili, prosessia ohjataan stabiilisti ja yhdenmukaisesti, prosessilla on omistaja ja prosessin keskiarvo on asetettu ”oikealla” tavalla kuten osissa I ja II on esitetty.

Oikeaa tapaa valittaessa kiinnittyy huomio prosessin suorituskykyyn ja suorituskykyindeksiin C_p eli suunnitteluvaatimukseen. Jos indeksi on C_p <1, silloin kohdan 4 ehto ei ole toteutunut ja vääjäämättä syntyy aina virheriski ja prosessin asetuksesta tulee vaativa ja kallis toimenpide. Taulukko 1. Prosessin luonnolliset rajat ovat tällöin suuremmat kuin tuotteen/palvelun spesifioidut toleranssit.

Prosessin luonnolliset rajat (LCL, UCL) on oltava spesifikaatiorajojen eli suunnittelurajojen sisäpuolella. Tällöin C_p>1. Luonnollinen raja on määritetty empiirisen kokemuksen (Emirical Rule) mukaan ja sovittu 3:ksi sigmaksi keskiarvosta^/1/. Ne eivät siis perustu suoran tuote tai palvelusuunnitteluun.

On kaksi tapaa parantaa prosessia suorituskykyä C_p:

• toleransseja, speksirajoja, levennetään niin paljon, että luonnolliset rajat sopivat rajoihin (kasvatetaan erotusta, USL-LSL). Tämä tarkoittaa usein myös asiakashävikin kasvamista tuotantohävikin pienenemisen kustannuksella.
• Muutetaan so. parannetaan prosessia niin, että luonnollista vaihtelua (σ_ST), sigmaa voidaan pienentää (pienennetään 6σ_ST:tä).

Motorola kehitti 1980-luvun alussa tekniikan nimeltä Six Sigma, jossa käytetään näitä molempia keinoja. Vuonna 1988 Motorola julkaisi perusteoksen Six Sigmasta^/2/, jossa sekä toleransseja ”levitetään” (Design for Six Sigma, DFSS) ja valmistusprosessin hajontaa pienennetään, ”parannetaan” (Six Sigma). Kuva 2

Six Sigman kehityksen pontimina oli alkujaan Japanin laadun kehittyminen ylivertaiseksi. Tästä kuvaavana esimerkkinä on saksalaisessa laatulehdessä Qualität and Zuverlässikeit (1992) julkaistu vertailu USA:n ja Japanin autotehtaiden laadusta. USA:ssa C_pk keskiarvo oli 1,2 vuonna 1990 ja Japanissa C_pk= 4,5. Suomessa taso on edelleen C_pk= 0,4 – 0,6. Asettamalla prosessi oikein, suorituskykyä voidaan merkittävästi parantaa lähelle C_p:tä pienentämällä eroa nominaali-prosessin keskiarvo (µ-x_av) (Huom: C_pk= C_p – (µ-x_av)/3σ_s, kun toleranssi on symmetrinen.

Six Sigman kehitys kulkenut paljon eteenpäin vuodesta 1987, jolloin Motorola rekisteröi Six Sigman ®. Huippuvaikeasta tekniikasta, joka vain ”parhaimmista parhaimmat” voivat hallita, kuten General Electric määritteli vielä 1990-luvun alussa. Nyt ollaan päädytty jokaisen omaksuttavissa olevaan kehitysmenetelmään kiitos Minitabin ja standardoinnin. Lisäksi Six Sigmaan on integroitu Lean vuonna 2002.

Lean Six Sigman ansiosta yritykset voivat nopeasti ja tehokkaasti asettaa prosessit, kun taataan C_p>2. Koneen ja prosessin keskiarvon asettaminen lähelle nominaalia voi tapahtua vain yhden näytteen perusteella ilman että on riski virheellisten tuotteiden tai palvelujen syntymiselle. C_p-indeksi ≥2 on myös lähes välttämätön automatisoidussa robottituotannossa, nopeissa vaihdoissa ja lyhyt-sarja-tuotanossa tai jopa Leanin yhden kappaleen virtauksessa (one piece flow) .

”Luonnollisen” sigman pienentäminen – kuinka saavuttaa C_p≥2

Luonnollinen sigma-käsite liittyy täydelliseen satunnaisuuteen ja stabiiliin satunnaisjakaumaan. Insinööri voi helposti muuttaa speksejä, suunnittelurajoja, mutta kuinka muuttaa sattuman synnyttämiä ”luonnollisia” rajoja?

Edelleen suurimassa osassa tilasto-, laatu- ja prosessitekniikan kirjoja sigma oletetaan ”mystisesti” vakioksi, jolle ei voida tehdä mitään. Ainoa mahdollisuus vaikuttaa sigmaan on valita toisenlainen tuotantoprosessi, kone jne! Näin uskottiin ja uskotaan edelleen! Laatu maksaa, tarvitaan parempia koneita vai tarvitaanko?

1950-luvulla Genichi Taguchi kehitti opin Robust Parameter Design, RPD (off-line quality control, parametrisuunnittelu), jolla pystyttiin saman prosessin sisällä muuttamaan tuotteen ja prosessin sigmaa ja asettamaan keskiarvo paikalleen. Tämä tekniikka esiteltiin USA:ssa 1980^/3/. Keskeistä oli pienentää tuotteiden ja prosessien varianssia, satunnaista vaihtelua eli signaali-kohinasuhdetta S/N.

Tämä oli läpimurto, joka johti myöhemmin myös Six Sigman kehittämiseen ja rekisteröintiin 7 vuotta myöhemmin tekniikan esittelystä USA:ssa. Keskeistä oli löytää ja ymmärtää, mikä tai mitkä tekijät voivat pienentää systeemin tai prosessin sisällä luonnollista satunnaista vaihtelua. Tiedettiin vanhastaan yksi keino, tiukemmat toleranssit, mutta samalla kustannukset nousevat radikaalisti.

Keskeiset fysikaaliset ilmiöt sigman pienenemiseen ovat tekijöiden välinen keskinäisvaikutus (interaction) ja parametrien epälineaariset efektit.

Mitä keinoja meillä on löytää kyseiset ilmiöt? Tavanomainen havainnointi ei –ainakaan lyhyellä aikajaksolla – mahdollista prosessin sisältä löytämään kyseisiä ilmiötä, koska tarvitaan vähintään kaksi muuttujaa. Informaation on tultava ”ulkoa”, valmentaja, ulkoinen opittu ”tieto tai taito”, toinen prosessi, menettelytapa jne.

On olemassa kuitenkin menetelmä, joka paljastaa systeemin parannus-mahdollisuuden. Se on DoE, Design of Experiments, monimuuttujakoesuunnitelma.
Alkujaan menetelmän kehitti R. A. Fisher vuosina 1925-35 tutkiessaan viljojen satoisuutta ja menetelmiä satoisuuden kasvattamiseen.

Tämä tekniikka on yhdistetty Six Sigmaan ja mainitaan myös ”The Nature of Six Sigma Quality” kirjasessa kuin myös Taguchi-menetelmä.

Genichi Taguchi tutki ja kehitti monimuuttujatekniikkaa 1940-luvulta lähtien. Syntyi ns. Taguchi-menetelmä ja ristimatriisitekniikka (Crossed Array Design) ja signaali-kohinasuhde.

Tämä” salainen” menetelmä oli myös Toyotan insinöörien ja Leanin taustalla. Taguchi työskenteli Toyotalla opettaen suunnitteluinsinöörejä. Kun lännessä säädettiin keskiarvoa, Toyotalla parannettiin suorituskykyä (C_p ->4,5, katso kuva 3) ja samalla oli mahdollista siirtyä nopeaan asetukseen (SMED), lyhyihin sarjoihin ja 0-virheeseen, koska asetuksen keskiarvovirhe ”häviää” ja asetukseen tarvitaan näyte n=1 kpl tai jopa 0. En usko, että Leania voi toteuttaa uskottavasti, jos prosessin suorituskyky ei ole vähintään C_p>1,67! Toyota ei turhaan asettanut laatua nro 1:ksi.

Kuinka työntekijät voisivat käyttää asetuksessa koesuunnittelua?

Asentajakoe (asetuskoe)

Ensimmäisen kerran törmäsin vakavaan asetusongelmaan Eimo-Muovilla 1980-luvun lopussa. Eimo valmisti lyhyissä sarjoissa teollisuusasiakkaille muoviosia, joiden oli oltava mittatarkkoja. Muotteja vaihdettiin ruiskupuristuskoneisiin lähes päivittäin. Siis lyhyitä sarjoja. Tämän jälkeen ajettiin kappaleita ja säädettiin ja säädettiin tunteja, vuoroja ja varsinainen tuotantoajo kesti vain muutaman tunnin.

Ongelma oli, että asentajan oli löydettävä lukuisten tekijöiden joukosta yhdistelmä, jolla mitat saatiin toleranssiin.

Esitin Eimon johdolle, että ajetaan jokaisen muotin osalta ns. Taguchi-koe. Tämän asentajat tyrmäsivät. Hetken mietittyäni esitin, että josko Eimo-koe kävisi ja laadin työntekijöille ”Asentajakoe” lomakesarjan ja ohjeen kuinka koe on suoritettava ja analysoitava. Tämä hyväksyttiin ja asetusajat lyhenivät dramaattisesti ja myös virheelliset tuotteet. Nimen muutos riitti hyväksymiseen! Kuvassa 2 todellista asentajakoetta L4 ja L8-matriisi. Asentajat itse laskivat ja analysoivat kokeet. Kokeen kesto tyypillisesti 15 min – 30 min. Asetusajat lyhenivät 1/10-1/100-osaan.

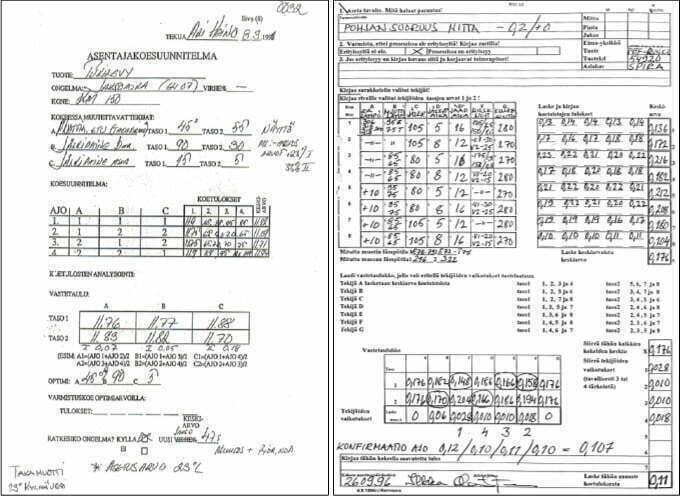
Sorvattavan kappaleen pinnan laatu

Seuraavassa yksinkertainen Kymen Ammattikorkeakoulussa toteutettu esimerkki prosessin suorituskyvyn parantamisesta, joka vastaa Eimon L8-koetta. Tutkimuksen kohteena on alumiinin lieriösorvaus ja asetuksen tavoitteena on saavuttaa mahdollisimman hyvä pinnan laatu Ra-arvo. Työn tekijät opettajat Asko Patana ja Jussi Manninen. Työ tehtiin vuonna 2007.

Esimerkki suorituskyvyn parannuksesta – alumiinin lieriösorvaus ja tasaisuus

• Tavoitteena koesuunnitelman avulla tutkia eri tekijöiden merkitystä sorvattavan kappaleen pinnankarheuteen ja saavuttaa työkappaleen mahdollisimman pieni pinnankarheus
• Työstön taloudellisuutta, teräkustannuksia ja työkappaleen lopullista mittatarkkuutta ei huomioitu tekijöitä valittaessa
• Sorvaustapahtumaksi valittiin ulkopuolinen lieriösorvaus
• Raaka-aineeksi valittiin alumiini, koska kokeessa käytettävän sorvin istukka on paineilmatoiminen eikä se siten mahdollista suuria lastuamisvoimia
• Käytettävissä kaksi alumiinin viimeistelysorvaukseen tarkoitettua terätyyppiä sekä kaksi erimallista teräpidintä

Syötön ja lastuamisnopeuden arvot valittiin terävalmistajan ohjearvojen ja ensimmäisen koesarjan perusteella.

Pinnankarheuteen ei ole yhtä säätötekijää, joten ongelma on ”suorituskyky” ongelma. Ryhmä ideoi tekijät, jotka voivat vaikuttaa pinnan karheuteen. Kuva 6.

Ryhmä valitsi punaisella merkityt tekijät monimuuttujatestaukseen eli DOE-kokeeseen. Six Sigmassa tekijöiden valinta tapahtuu Mittaus-Analyysi -vaiheessa.

• Koe suoritettu 19.12.2006 – 2.1.2007
• Paikka: Kymenlaakson ammattikorkeakoulu, Metsolan toimipiste konetekniikan laboratorio
• NC-ohjattava sorvi EMCOTURN 120P (kuva 7)

Testattavat tekijät ja niiden tasot:

Koesuunnitelma L8-koodatussa muodossa ja koetulokset (kuva 9)

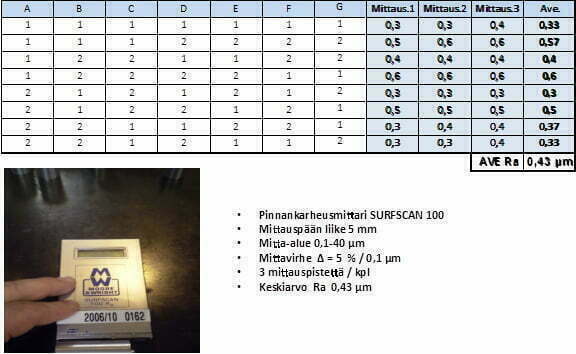
Koska koesuunnittelumatriisi on ortogonaalinen, voidaan ulostulot palauttaa sisäänmenoihin ja tarkastella, mitkä tekijämuutokset vaikuttavat ja kuinka paljon (erotus ja järjestys). Tätä kutsutaan vastetauluksi (Kuva 10).

Kaikkein eniten vaikutti syötön muutos ja vähiten rasvan poiston muutos. Suositus kertoo pinnan tasaisuuden optimin (minimi karheuden) tässä testissä. Tälle voidaan laskea ennuste (kuva 11).

Johtopäätös: Konfirmaatiokokeessa saamamme profiilin keskipoikkeama Ra = 0,27 µm ei täysin toteuttanut ennustettua Ra – arvoa 0,24 µm mutta ottaen huomioon pinnankarheusmittarin virherajan, Δ = 5 % lukemasta tai 0,1 µm (kumpi suurempi), tulosta voidaan pitää ennusteen mukaisena.

Ensimmäisen koesarjan tulosten perusteella olimme jättäneet tekijöitä pois, joilla emme todenneet olevan vaikutusta kappaleen pinnankarheuteen. Lisäksi ensimmäisen koesarjan tulosten perusteella pystyimme valitsemaan lastuamisparametrit niin, että lopputuloksena saatua pinnankarheutta Ra = 0,27 µm voidaan pitää erittäin onnistuneena. (kokeen tekijöiden kommentti).

Yhteenveto

Keskiarvon säätäminen oikein on keskeistä asetettaessa niin palvelu kuin tuoteprosesseja, niissä olevia linjoja, koneita ja jopa erilaisia menettelyjä.

Silloin kun säätö voidaan toteuttaa yhdellä muuttujalla, säätimellä, on tiedettävä kuinka monta näytettä on otettava ja lasketusta keskiarvosta on pääteltävä kriittisen arvon Δσ avulla, onko säätöä suoritettava vai ei. Jos säädön suorittaa pienemmästä arvosta kuin taulukko osoittaa, seuraa turhaa työtä ja lisää vaihtelua.

Mitä huonompi/pienempi on prosessin suorituskyky C_p , sitä vaativampaa on prosessin keskiarvon säätäminen. Tarvitaan suurempia näytemääriä, laskentaa ja työtä ja aikaa, jotta päästään erinomaiseen laatuun. Tämä onnistuu vain suurilla sarjoilla ja minimi määrällä asetuksia.

Jos säätävää tai ohjaavaa tekijää ei ole tiedossa, se tai ne voidaan etsiä käyttämällä Lean Six Sigma -menettelyä (ISO 13053). Tyypillisesti prosessissa on 100-1500 erilaista tekijää, joiden joukosta tekijät on mahdollista ”kaivaa” esille.

Oleellista kuitenkin on, että tekijöitä ei saada ”näkyviin” muuttamalla yhtä tekijää kerralla (OFAT-testi). Satunnainen vaihtelu ”estää” signaalin havaitsemisen. Siksi on käsiteltävä ”kaikkia” tekijöitä samanaikaisesti. Uusin tekniikka tällä alalla on ns. DSD-suunnitelmat^/5/, joilla voidaan tehokkaasti screenata tekijät ja optimoida lopputuloksen.

Prosessin suorituskyvyn nostamiseen kannattaa aina. Vältytään monimutkaisilta ja pitkiltä asetusmenettelyiltä ja säätö on mahdollista toteuttaa jopa yhdellä kappaleella.

Lähteet:

1. Walter A. Shewhart: Economic Control of Quality of Manufactured Products, 1931
2. Mikel J. Harry: The Nature of Six Sigma Quality, 1988
3. Genishi Taguchi, Y. Wu: Introduction to Off-Line Quality Control, 1980
4. Donald J.Wheeler, Davis S. Chambers: Understanding Statistical Process Control, SPC Press, 1986
5. Eero E. Karjalainen. Artikkeli: Onko DSD-koesuunnitelmat vuosisadan merkittävin parannus- ja koesuunnitteluinnovaatio?
6. Eero E. Karjalainen. Artikkeli: Prosessin ja työkoneen säätäminen ja asettaminen – OSA I
7. Eero E. Karjalainen. Artikkeli: Prosessin ja työkoneen säätäminen ja asettaminen – OSA II

Lue koko artikkelisarja:

1. Prosessin ja työkoneen säätäminen ja asettaminen – OSA I, 2017
2. Prosessin ja työkoneen säätäminen ja asettaminen – OSA II, 2017
3. Prosessin ja työkoneen säätäminen ja asettaminen – OSA III, 2017
4. Prosessin ja työkoneen säätäminen ja asettaminen – OSA IV, 2017