Artikkelisarjan ensimmäisessä osassa käsittelin vaihtelua yleisesti, toisessa osassa paneuduin tarkemmin vaihtelun merkitykseen. Kolmannessa osassa pyrin yhdistämään vaihtelun joihinkin yleisesti käytettyihin termeihin ja kuvaamaan sen ymmärtämiseen liittyviä haasteita.
Leanin yhteydessä tavoitteeksi mainitaan usein asiakkaan kokeman arvon lisääminen ja tämän aikaansaaminen hukkaa vähentämällä. Mistä tässä on kyse?
Perinteisesti hukat jaetaan 7 (tai 8) eri luokkaan: Ylituotanto, ylimääräinen varastointi, odotus, ylimääräinen kuljetus, ylimääräinen liike, yliprosessointi ja viat. Mitä nämä ovat?
Odotus on selkeästi aikaa.
Ylituotanto ja ylimääräinen varastointi, no ne ovat varastoa. Jos tuotetaan jotain ylimääräistä, niin se pitää varastoida.
Ylimääräinen kuljetus, ylimääräinen liike, yliprosessointi ja viat ovat asioita, jotka jonkun pitää tehdä, eli ne kuluttavat kapasiteettia.
Eli hukkaa on aika, varasto ja kapasiteetti. Kuulostaako tutulta?
Tehdasfysiikan mukaan systeemi suojautuu vaihtelua vastaan (eli vaihtelu aiheuttaa) jollain yhdistelmällä aikaa, varastoja ja kapasiteettia.
Itse asiassa Toyotan tuotantojärjestelmässä ja sitä kautta Leanissa ei rajoituta pelkästään yllä mainittuihin 7 hukkaan, vaan koko käsite on laajempi. Näiden mainittujen hukkien (Muda) lisäksi Toyotan tuotantojärjestelmä tunnistaa myös ylikuormituksen (Muri) ja vaihtelun (Mura) osaksi hukkakokonaisuutta. Tämäkin alkaa kuulostaa tutulta, Kingmanin kaava, mm. tehdasfysiikan kautta tutuksi tullut.
CT=VUT, eli jaksoaika on riippuvainen vaihtelusta, kuormituksesta ja työhön tarvittavasta ajasta.
Jaksoaika on vaikkapa aikaa, joka joudutaan odottamaan ennen prosessiin pääsyä tai joidenkin prosessin vaiheiden välillä (eli hukka-termein odotusta). Ja Sir Kingman kertoo meille, että tämä hukan tyyppi on seurausta jostain, vaihtelusta, kuormituksesta ja työhön tarvittavasta ajasta. Lisää tästä vaikkapa Antti Piiraisen kirjoittamasta artikkelista: Kaizen, Ohno ja VUT.
Miksi vaihtelun ymmärtäminen on sitten niin vaikeaa?
Otetaan esimerkiksi jokin meitä kiinnostava prosessi ja aletaan tutkia sen tuotosta, mitataan sitä. Ennemmin tai myöhemmin meille kertyy tietty määrä mittausten tuloksia, vaikkapa seuraavasti (suuruusjärjestyksessä): 3, 4, 4, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 9, 9, 9, 9, 9, 10, 10, 11.
Pelkkä numeroiden tuijottelu ei ole kovin mielenkiintoista taikka hyödyllistäkään, monesti tällaisessa tilanteessa halutaan laskea tuloksista jotain, tunnuslukuja, eräänlaisia yksinkertaistuksia. Eniten käytetty ja monille tuttu yksinkertaistus on varmaankin keskiarvo. Katsotaan tilannetta kuvien kautta.
Kun aikaisemmin saadut tulokset piirretään näkyviin, tilanne näyttää tältä:
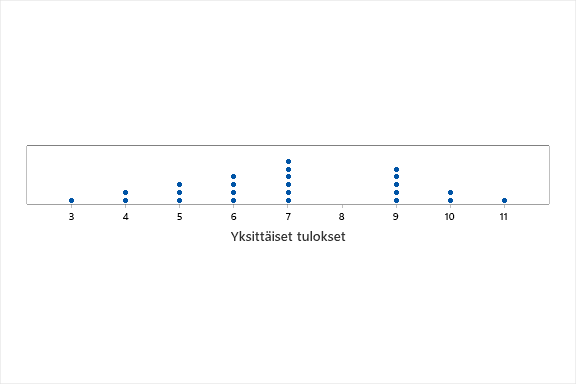
Keskiarvo on yksinkertaistaa tulokset yhteen lukuarvoon, jonka voisi ajatella olevan se piste, johon kaikki tulokset voisi sijoittaa ilman että tulosten ”painopiste” muuttuisi mitenkään. Tuloksista laskettu keskiarvo on 7 ja kuvana tämä ”kaikkien tulosten sijoittaminen” näyttää tältä. Eli keskiarvo on eräänlainen tasapainopiste tuloksille.
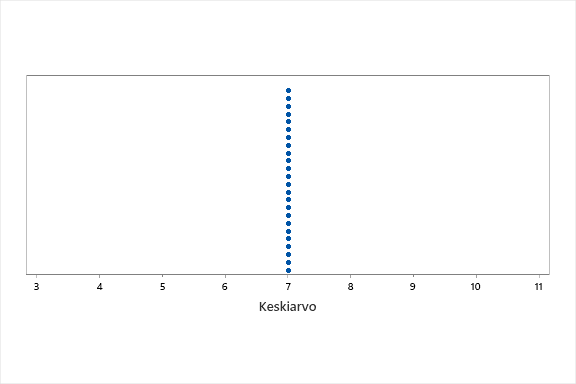
Ja kuten kuvista nähdään, pelkkä keskiarvo, vaikka onkin monille tuttu, ei kerro mitään siitä, miten tulokset ovat hajaantuneet tämän tasapainopisteen ympärille (eli vaihtelusta). Tämä ei tietenkään tee keskiarvosta tarpeetonta, mutta yksinään se kertoo vain osan meitä kiinnostavista asioista.
Keskiarvon jälkeen seuraavaksi eniten käytetty tunnusluku eli yksinkertaistus on keskihajonta, joka määritelmän mukaan on hajontaa kuvaava parametri. Keskihajonta kuvaa tilanteessanne tuloksien keskimääräistä etäisyyttä niiden omasta keskiarvosta. Myös varianssi tulee nopeasti vastaan, kun aletaan puhumaan hajontaa kuvaavista parametreistä. Jotkut saattavat muistaa termit kouluajoilta, mutta onko ollut tarvetta käyttää sen jälkeen? Yritetään havainnollistaa keskihajontaa ja varianssia menemättä kuitenkaan varsinaiseen laskentaan.
Käytetään samoja tuloksia kuin keskiarvon tutkinnassa. Tuloksien perusteella laskettu arvo keskihajonnalle on 2 (voit toistaa tämän esimerkiksi Excelillä käyttäen KESKIHAJONTA.P-funktiota). Muodostetaan nyt uusi kuva, johon jaamme alkuperäiset 24 havaintoa kahteen 12 havainnon ”pinoon”. Toinen pino on kohdassa 5 (keskiarvo – keskihajonta) ja toinen pino kohdassa 9 (keskiarvo + keskihajonta), Tällä uudella kuvalla on sama keskiarvo (7) ja sama keskihajonta (2) kuin alkuperäisistä tuloksista muodostetulla kuvalla. Eli mielikuvaharjoituksena siirretään alkuperäiset tulokset kohtiin 5 ja 9 → sama keskiarvo ja keskihajonta kuin alkuperäisellä datalla, tunnuslukujenhan oli tarkoitus yksinkertaistaa.
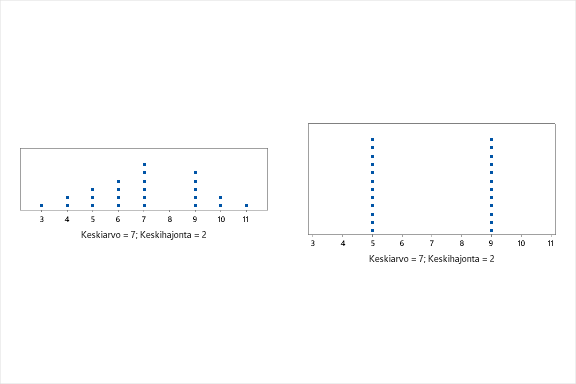
Keskihajonnan voidaan siis ajatella kuvaavan keskimääräistä etäisyyttä, jonka päähän keskiarvosta havaintomme voidaan pinota ja samalla säilyttää keskiarvo ja keskihajonta samoina.
Jos pyöräytämme tätä juuri muodostamaamme kahdesta pinosta koostuvaa yksinkertaistustamme x-tasossa keskipisteensä (keskiarvon) ympäri, saamme aikaan ympyrän, jonka pinta-ala on 4π, (ympyrän pinta-ala = πr2, tässä r = keskihajonta = 2).
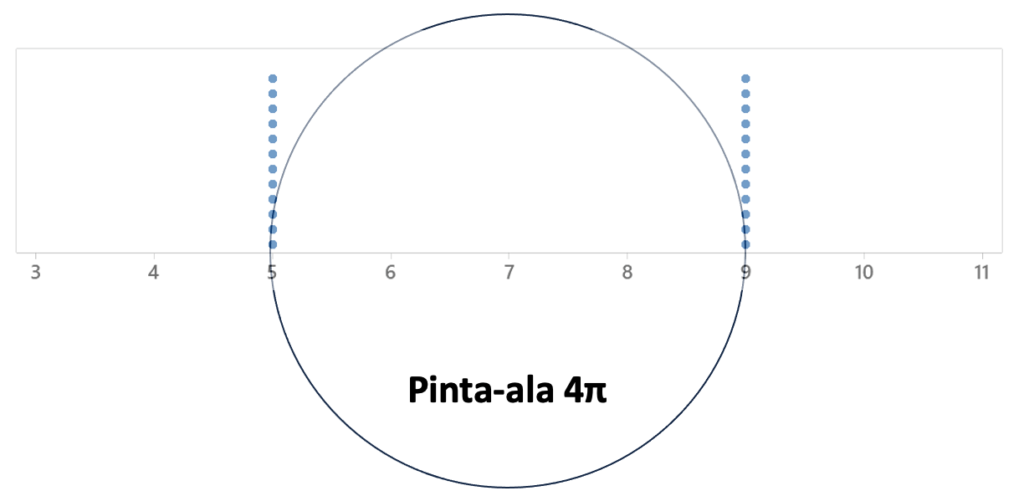
Tämä muodostunut pinta-ala on itse asiassa seuraava yksinkertaistus alkuperäisistä tuloksistamme, siitä käytetään nimeä varianssi. Tilastotieteessä varianssi tunnetaan myös nimellä toinen keskusmomentti (keskihajonta on se ensimmäinen). Varianssin tulkintaa hankaloittaa vielä se, että sen yksikkö on alkuperäisten tulosten yksikkö korotettuna toiseen potenssiin (pinta-ala), keskihajonta on helpompi sisäistää, koska sen yksikkö on sama kuin mitattujen tulosten.
Vaihtelu ja sitä kuvaavat keskihajonta ja varianssi ovat huomattavasti vähemmän tunnettuja kuin keskiarvo. Jos asiaa ei tiedä, miten siihen voi reagoida? Ei oikein mitenkään. Myron Tribus kuvaa tätä ongelmaa hyvin tekstissään ”The Germ Theory of Management”. Muutama poiminta siitä ja linkki tekstiin lähteissä.
Lääketiedettä harjoitettiin jo pitkään ennen kuin tietoa erilaisista mikro-organismeista oli edes olemassa. Osa potilaista kuoli, osa parani ja osaan potilaista erilaisilla hoidoilla ei ollut vaikutusta. Oli kehitetty erilaisia teorioita sairauksien syistä, malaria (mala aria kesk. ital. paha ilma) aiheutui soisten alueiden pahan laatuisesta ilmasta, miasmasta.
Lääkärit hoitivat potilaita parhaan kykynsä mukaan perustuen siihen, mitä he olivat koulussa ja kokemuksen kautta oppineet. He pystyivät soveltamaan vain sitä, mitä tiesivät ja mihin uskoivat. Sitä mitä ei tiedä ei voi soveltaa.
Tänään saattaa ihmetyttää se, että vielä 200 vuotta sitten haavan ompelun jälkeen kirurgit suosittelivat jättämään langanpätkän haavan ulkopuolelle. Tämä tehtiin siksi, että mätä voisi valua ulos haavasta, varma seuraus sterilisoimattoman langan käytöstä pesemättömillä käsillä ja sterilisoimattomalla neulalla.
Lääketiede on päässyt pitkälle vuosien saatossa, taudinaiheuttajista tiedetään nykyään paljon enemmän kuin 1800-luvulla ja monia tauteja voidaan menestyksekkäästi hoitaa. Mutta vertaus on edelleen ajankohtainen, kun puhutaan vaihtelun ymmärtämisestä, jos et tiedä mistä on kyse, miten voisit reagoida siihen? Vaihtelun seuraukset ovat kaikille tuttuja, mutta onko syy? Ymmärretäänkö vaihtelua?
Yhteyttä vaihtelun ja silmällä näkymättömien taudinaiheuttajien välillä voi toki miettiä lisääkin. Jos et ole ikinä kuullutkaan vaihtelusta tai taudinaiheuttajista et tietenkään voi reagoida niihin mitenkään (unknown unknown). Tämä ei päde teihin, olette jo kuulleet vaihtelusta. Toinen vaihtoehto on, että tiedät vaihtelun (tai taudinaiheuttajien) olevan olemassa, mutta et mitään muuta (known unknown). Tässäkin tilanteessa toimenpiteet ovat mahdottomia (tai niitä ei ainakaan kannata tehdä, koska et tiedä mitä tehdä), mutta aiheeseen tarkempi tutustuminen ja oikean reagointitavan löytäminen on mahdollista.
Kolmantena vaihtoehtona on mahdollista, että olet joskus tiennyt asian (eli vaikkapa vaihtelun olemassaolon ja vaikutukset), mutta se on päässyt unohtumaan (unknown known). Toimenpiteet ovat mahdottomia, mutta jos kuulet termit uudestaan asia saattaa palautua mieleen (tai pienen kertauksen kautta). Neljäs vaihtoehto on ainoa, jossa toimenpiteet ovat mahdollisia, muistat asian ja tiedät miten toimia (known known) ja tätä neljättä osuutta pitää tietenkin tärkeiden asioiden kannalta pyrkiä aktiivisesti laajentamaan.
Tässä tuli itse asiassa kuvattua eräänlainen versio JOHARI-ikkunasta, yksi kohtuullisen kuuluisa näkemys tästä on Yhdysvaltojen silloisen puolustusministerin Donald Rumsfeldin puhe vuodelta 2002, kannattaa tutustua.
Tehdään pieni ajatusharjoitus. Ajattele mitä tahansa sinulle tutun tuotteen ominaisuutta tai jonkin prosessin ulostuloa, tuotosta. Ja jos haluat lisätä vaikeusastetta, mieti vielä, miten tämä ominaisuus tai ulostulo voi vaihdella.
Kun olet saanut valittua tämän ominaisuuden tai ulostulon, listaa mielessäsi kaikki mahdolliset syy-seuraussuhteet, jotka voivat vaikuttaa jollain tavalla siihen. Tyypillisesti listalla on kymmeniä tai satoja mahdollisia syitä (ja tarkoitushan oli näyttää, että lista on pitkä, ei mennä sen yksityiskohtiin).
Oli listalla sitten kymmeniä tai satoja syitä lienee selvää, etteivät kaikki listatut syyt vaikuta yhtä paljoa kohteenasi olevaan ominaisuuteen tai ulostuloon. Joillain syillä on suuri vaikutus ja toisilla sitten pieni. Jos omaisimme täydellisen tietämyksen jokaisen syyn vaikutuksesta, voisimme järjestää kaikki syyt niiden vaikutuksen perusteella.
Useimmissa tapauksissa tulos olisi sellainen, jossa muutama harva syy aiheuttaa valtaosan vaikutuksista seuraukseen. Tallaisesta tuloksesta piirrettyä kuvaa kutsutaan Paretoksi, idean kehittäjän mukaan.
Ensimmäinen oppi tästä kuvasta on se, että jos pystymme ohjaamaan neljää ensimmäistä syytä, voimme ohjata valtaosaa seurauksen (eli ominaisuuden tai prosessin ulostulon) vaihtelusta (yli 80 % tässä tapauksessa). Mutta vain, jos tiedämme mitkä nämä neljä oleellista syytä ovat.
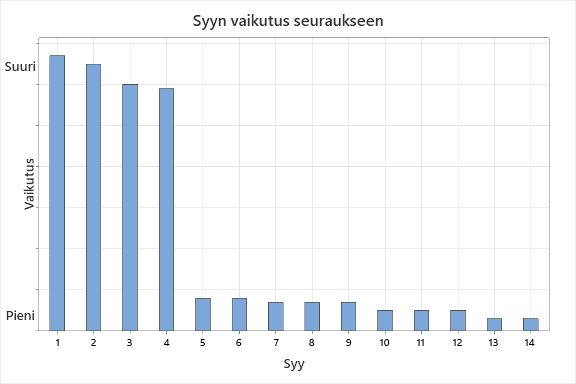
Toinen kuvasta esiin nouseva huomio on se, että saavutettavat hyödyt vähenevät nopeasti. Jos oletetaan, että jokaisen neljän ensimmäisen syyn ohjaaminen maksaa saman verran kuin neljän seuraavan ja nähdään, että toisaalta neljän seuraavan vaikutus on vain murto-osa neljän ensimmäisen vaikutuksesta, saatava hyöty suhteessa lisäpanostukseen on minimaalinen.
Yhteenveto
Tästä ja aikaisemmista vaihtelua käsitelleistä artikkeleista:
- Vaihtelun ymmärtäminen on kriittisen tärkeä osa johtamista ja parantamista.
- Kaikki työ tapahtuu jossain prosessissa ja kaikissa prosesseissa on vaihtelua.
- Vaihtelu heikentää laatua, pidentää jonoja, aiheuttaa kustannuksia, aiheuttaa reklamaatioita, heikentää asiakastyytyväisyyttä, tiivistettynä vaihtelu heikentää systeemin suorituskykyä.
- Vaihtelun ymmärtäminen (satunnaista vaihtelua vai jostain erityisestä syystä johtuvaa) johdattaa oikean menetelmän äärelle.
- Pelkkä lukujen tuijottelu tai keskiarvojen ihmettely ei riitä, tarvitaan jotain muuta.
- Vaihtelu prosessin ulostulossa on seurausta sisäänmenojen vaihtelusta, ja jollain tavalla nämä syyt on selvitettävä, jos vaihtelua halutaan vähentää.
Lähteet:
- Toyota Production System, Ohno Taiichi, CRC Press 1988.
- Gemba Kaizen, Imai Masaaki, McGraw-Hill 1997.
- Mura, Muri, Muda? Womac James, https://www.lean.org/the-lean-post/articles/mura-muri-muda/ (vierailtu 6.2.2024).
- What Are the Variance, and Standard Deviation? Wheeler Donald J., https://www.spcpress.com/pdf/DJW386.pdf(vierailtu 13.2.2023).
- The Germ Theory of Management, Tribus Myron, http://www.qla.com.au/pathtoitems/germ_theory.pdf (vierailtu 13.2.2024).
- Systems Thinking – And Other Dangerous Habits, Dettmer, H. William, Virtualbookworm.com 2021.
- Twenty Things You Need To Know, Wheeler Donald J., SPC Press 2009.
- Pareto principle, https://en.wikipedia.org/wiki/Pareto_principle (vierailtu 27.2.2024).
Tutustu kurssitarjontaamme!
Tilaa uutiskirje
Liity postituslistalle ja saat uusimmat artikkelit suoraan sähköpostiisi.
Tämä lomake on suojattu Google reCAPTCHA:lla. Lue tietosuojaseloste ja käyttöehdot.
Liittymällä postituslistalle hyväksyt Quality Knowhow Karjalainen Oy:n tietosuojaselosteen ja Quality Knowhow Karjalainen Oy voi lähettää sinulle ajankohtaisia artikkeleita, videoita sekä tietoa ja tarjouksia kursseista, kirjoista sekä ohjelmistoista.




Tämä lomake on suojattu Google reCAPTCHA:lla. Lue tietosuojaseloste ja käyttöehdot.