Vaihtelun ymmärtäminen – osa 4

Vaihtelun ymmärtäminen – osa 4

Vaihtelua olen käsitellyt aikaisemmissakin artikkeleissa (Vaihtelun ymmärtäminen: osa 1, osa 2 ja osa 3), ne kannattaa palauttaa mieleen ennen tähän artikkeliin paneutumista. Vaihtelun vaikutus laatuun ja tuottavuuteen on tullut selväksi ja keskiarvo, keskihajonta ja varianssikin ovat jo tuttuja. Miten tätä kertynyttä tietämystä sitten voidaan käyttää ohjaamaan päätöksentekoa? Dataan perustuvasta päätöksenteosta puhutaan paljon, mutta mitä tämä voisi tarkoittaa, kun mukaan otetaan vaihtelu? Siitä lyhyt esimerkki seuraavaksi.

Kuvitellaan, että olemme tehtaassa. Tehdas tuottaa tuotteita ja käyttää tässä apuna konetta. Konetta pitää huoltaa määräajoin, jotta se toimii moitteettomasti. Huolto voi tarkoittaa esimerkiksi puhdistusta, säätöä, rasvausta, kuluvien osien vaihtoa yms. ylläpitoa. Tämänhetkinen tapa toimia on seuraava: ajetaan konetta 70 tuntia ja pysäytetään se 10 tunniksi huoltoa varten ja ajetaan taas 70 tuntia jne. Kaikki toimii koneen suhteen hyvin, ei yllättäviä ongelmia ja toimintatapa on kunnossapidon kannaltakin mukava (määräajoin, 2 viikon välein tehtävä toimenpide).

Aloitejärjestelmä tuottaa idean, jossa ehdotetaan toimintatavan muuttamista. Jos huolto pilkottaisiin pienempiin palasiin ja tehtäisiinkin vain 3,5 tunnin välein, aikaa yhteen toimenpiteeseen tarvittaisiin vain 30 minuuttia (0,5 h) ja vaikutus olisi tasan sama kuin harvemmin tehtävällä mutta pitkällä huollolla. Kysymys onkin, kannattaako siirtyä ehdotettuun lyhyempään huoltoväliin? (ja toisena tietenkin pitääkö aloitepalkkio maksaa?)

Joillain varmaan tulee heti mieleen, että ei todellakaan kannata tehdä huoltoja useammin, mitä harvemmin, sitä parempi. Onkohan näin, tutkitaan tilannetta datan avulla…

Koneiden kannalta yksi tärkeimmistä mittareista on niiden käytettävyys (A – Availability). Käytettävyys on suhdeluku, joka kuvaa kuinka suuren osan ajasta kone on käytössä, ja se lasketaan perinteisesti:

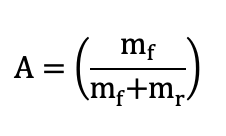
jossa:                 

A = käytettävyys

m_f = keskimääräinen aika vikaantumiseen (mean time to failure)

m_r = keskimääräinen korjaamisaika (mean time to repair)

Vaikka konetta ei tilanteessamme ajetakaan vikaantumiseen saakka, voimme kuitenkin olemassa olevilla tiedoilla laskea käytettävyydelle arvot sekä nykytilanteessa, että ehdotetussa lyhennetyn huoltovälin tilanteessa. Konetta pitäisi pystyä ajamaan koko ajan, mutta suunnitellut huollot syövät tätä aikaa, käytettävyys kertoo, kuinka paljon aikaa menetetään. Mitä lähempänä ykköstä ollaan, sitä parempi.

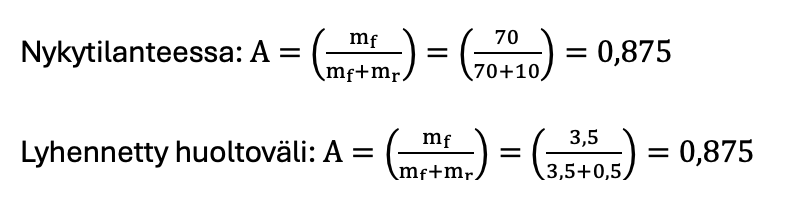
Tasan samat tulokset! Tarkoittaako tämä nyt sitä, että molemmat toimintatavat ovat yhtä hyviä? Ei välttämättä, artikkelin aihe oli vaihtelun ymmärtäminen, emmekä ole käsitelleet itse asiaa vielä lainkaan. Eikä unohdeta tuota käytettävyyttäkään, sitä tarvitaan vielä.

Saatatte muistaa, että vaihtelua kuvaavia tunnuslukuja oli useita, yksi eniten käytetyistä tottelee nimeä keskihajonta ja kun halutaan olla tehokkaita, eikä joka kerta kirjoittaa montaa kirjainta, keskihajonnan tunnuksena käytetään kreikan sigma kirjainta σ. Eri asioilla on eri suuruisia keskihajontoja, nyt haluaisimme selvittää, kumpi toimintatapa on vaihtelun kannalta parempi (eli vähemmän vaihtelua). Keskihajonta on siitäkin hankala, että eri asioiden keskihajontoja ei oikein voi verrata toisiinsa, vähän kuin vertaisi omenoita ja banaaneita. Jossain tilanteessa keskihajonnan arvo 10 on suuri, jossain toisessa tilanteessa sama lukuarvo 10 on mitätön.

Tarvitaan siis mittatikku, jonka avulla verrata asioita toisiinsa vaihtelun suhteen. Onneksi tällainen on olemassa, tunnetaan nimellä vaihteluvakio (coefficient of variation – c). Vaihteluvakio tarkoittaa yksinkertaisesti meitä kiinnostavan asian keskihajonnan ja keskiarvon suhdetta.

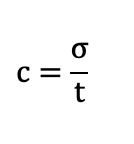
jossa:                 

c = vaihteluvakio

σ = keskihajonta

t = keskiarvo (t sen takia, että meitä tyypillisesti kiinnostaa aika, t=time)

Vaihtelun määrää voidaan arvioida vaihteluvakion avulla, jos c < 0,75 on vaihtelua vähän, jos c > 1,33 on vaihtelua paljon ja jos ollaan näiden välillä, tilanne on sellainen medium. Joissain tilanteissa (itse asiassa aika useinkin) käytetään ns. neliöllistä vaihteluvakiota, joka on siis c².

Seuraavaksi tarvitaan kohteena olevasta koneesta hieman dataa, täytyy mennä kellottamaan toimintaa. Tavoitteena on saada selville kuinka paljon koneelta tarvitaan aikaa yhden tuotteen tekemiseen, eli kello lähtee käyntiin, kun työ aloitetaan ja pysähtyy kun työ on valmis. Kun näitä mittauksia kertyy useampia, voidaan niistä laskea koneen luonnollinen prosessointiaika (t₀), siis kellotuksien keskiarvo ja saman ajan keskihajonta (σ₀). Useimmissa prosesseissa tämä luonnollinen vaihtelu on pientä ja siten c₀ < 0,75.

Oletetaan, että kohteena olevan koneen t₀ = 12 min ja σ₀ = 4 min. Nämä luvut eivät siis ota huomioon käytettävyyden vaikutusta. Kun käytettävyys otetaan huomioon, aletaan puhua tehollisista arvoista, esim. tehollinen prosessointiaika. Eli vaikka koneelta kellotettu aika on keskimäärin 12 minuuttia, pitkän ajan yli tutkittuna (eli ajan, joka sisältää myös määräajoin toteutettavat huollot), aika onkin jotain muuta. Käytettävyyden vaikutus prosessointiaikaan saadaan selville kaavalla:

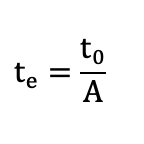
jossa:                 

t_e = tehollinen prosessointiaika

t₀ = luonnollinen prosessointiaika

A = käytettävyys

Eli esimerkissämme: 

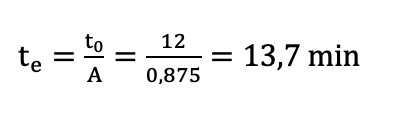
Myös keskihajonnalle voidaan laskea teholliset arvot, mutta palautetaan mieleen, mikä oli tutkimuksemme tarkoitus, selvittää mikä olisi huoltovälin lyhentämisen vaikutus vaihteluun. Tähän asioiden vertailuun tarvitaan aiemmin mainittua neliöllistä vaihteluvakiota. Itse asiassa tarvitsemme neliöllistä tehollista vaihteluvakiota, joka ottaa huomioon käytettävyyden vaikutuksen ja tarvittaessa myös huoltoon tarvittavan ajan vaihtelun.

Neliölliseen teholliseen vaihteluvakioon päästään kiinni tämän kaavan kautta:

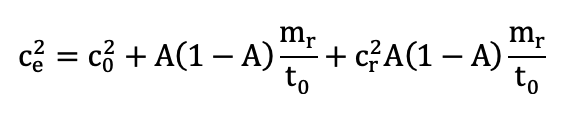
Näyttää hieman monimutkaiselta, mutta kaikki muu onkin jo tuttua, paitsi c_r², joka on huoltoon tarvittavan ajan neliöllinen vaihteluvakio. c_r² saataisiin selville kellottamalla tehtyjä huoltoja ja laskemalla näistä ajoista saadun keskihajonnan ja keskiarvon toinen potenssi. Oletetaan tässä, että huoltoon tarvittava aika ei vaihtele, eli että se on joka kerta joko tasan tarkkaan 10 tuntia tai tasan 30 minuuttia. Kun c_r² = 0, niin kaava yksinkertaistuu:

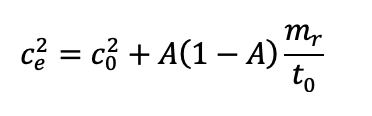
Tämän jälkeen ei muuta kuin lasketaan tulokset eri tilanteille ja katsotaan miten kannattaa toimia.

Ja jos yllä olevat vielä muutetaan vaihteluvakioiksi (pois neliöllisestä esitystavasta), niin voimme virallisesti lausua onko kussakin tilanteessa vaihtelua vähän vai paljon.

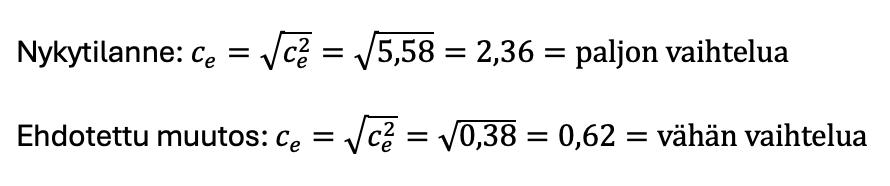
Vaihtelun kannalta pitkään kestävä huolto on ongelmallisempi kuin lyhyempi, tässä tilanteessa noin 4 kertaa hankalampi. Ja kuten kaavasta voi huomata, tekijä joka eron kahden toimintatavan välille aiheutti, oli huollon kesto (10 tuntia vs. 30 minuuttia). Tämä havainto voidaan yleistää ja yksinkertaistaa toteamalla, että lyhyet seisokit ovat laadun ja suorituskyvyn kannalta parempia kuin pitkät. Ja samaan hengenvetoon on syytä todeta, että kyseessä oli yksinkertaistus, tosielämässä vaikuttavat reunaehdot tekevät asiasta hieman monimutkaisemman.

Saman tyyppisesti voisimme tutkia vaikkapa töiden vapauttamisen vaikutusta vaihteluun. Onko merkitystä sillä, vapautetaanko kaikki päivän työt kerralla (suuri erä), vai vähitellen päivän aikana (pienempi erä)? Jätetäänpä tämä lukijoiden pohdittavaksi, tulos saattaa yllättää.

Päätösten tekeminen kannattaa perustaa datalle, mutta tämä ei vielä kaikissa tilanteissa riitä. Myös vaihtelu, jota on kaikkialla, pitää ymmärtää. Kun tähän lisätään vielä riittävät perustiedot prosessien lainalaisuuksista, voidaan selvittää eri asioiden vaikutus vaihteluun, eli laatuun ja suorituskykyyn, punnita eri vaihtoehtoja, sekä tehdä oikeasti dataan perustuvia päätöksiä, eikä vain arvailla.

Lähteet:

• Factory Physics 3^rd ed., Wallace J. Hopp, Mark L. Spearman (2011)
• Running Today´s Factory, Charles Standard, Dale Davis, Carl Hanser Verlag (1999)

Factory Physics, 3rd edition

175,00 € + alv (10%)