Älä hanki isompia vasaroita – varmista komponenttien suorituskyky ja estä hukka ennakkoon!

Hakataanko komponentteja kiinni toisiinsa isolla vasaralla jatkuvasti? Onko prosessin laaduntuottokyvyn vaatimukset osoitettu oikeilla menetelmillä uskottavasti ja mitä ihmettä ne tarkoittavat? Johdetaanko laatua niin, että ihmisillä on mahdollisuus tehdä työnsä ja onnistua? Eihän nykyiset menetelmät ja huono kommunikointi myynnin kanssa vie onnistumisen iloa? Onko varmistettu toimittajaa valittaessa, että oma kokoonpano voi tehdä työt kerralla valmiiksi ja voi onnistua joka kerta valitun toimittajan komponenteilla?

Tässä artikkelissa käsitellään PPAP vaatimuksia ja prosessin kyvykkyyden osoittamisen merkitystä ja toteutusta Minitab-ohjelmistolla, sekä keskeisiä sekaannuksen mahdollisuuksia tulosten tulkinnassa.

Mikä PPAP?

Perinteisessä valmistavassa teollisuudessa ja komponenttien alihankinnassa ei ole epätyypillistä, että toimittaja sitoutuu jonkinlaiseen ostajan määrittämään osien hyväksymismenettelyyn. Tämä ”dokumenttihirviö” on tunnettu paremmin lyhenteeltään PPAP (Production Part Approval Process) ja sen sisältö voi vaihdella ostajan harkinnan, toimittajan osoittaman luottamuksen tai tavaran luonteen mukaan, mutta tyypillisesti se kattaa erilaista suunnittelun dokumentaatiota ja määritystä, sekä todisteita erilaisista laatutekniikan perusmenetelmistä, kuten mm. mittaussysteemin analysointia, riskien arvioinnista, prosessin suunnittelusta, sekä prosessin stabiilisuuden ja suorituskyvyn todisteet.

Yleensä siis joukko enemmän tai vähemmän tuttuja kirjainten yhdistelmiä, joiden jonkinasteinen ymmärrys pitäisi olla myös varsinaista osien hankintaa tai niiden myyntiä tekevillä henkilöillä. Perusongelma on kuitenkin sama kuten esiteollisena aikana, eli miten saada eri toimittajien komponentit osumaan hyvällä todennäköisyydellä toisiinsa ilman ylimääräistä työstämistä. Mielellään joka kerta. Ennen tähän käytettiin tarkastusta, nykyään pitäisi käyttää jakaumien ajatusta ja tietoa prosessien vaihtelusta. Perusongelmaa on kuvattu kuvassa 1 alla. Eri paikoissa eri aikoina tehdyt osat pitäisi saada osumaan paikalleen kokoonpanossa, jos asia ei onnistu yritetään uudelleen tai haetaan iso, isompi ja lopulta isoin vasara.

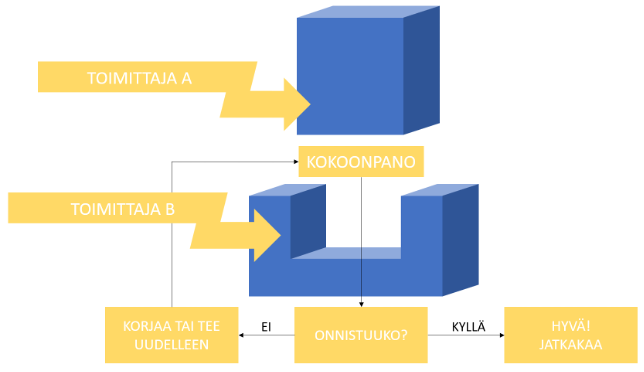
Tämä oli ongelma aikanaan myös Eli Whitneyllä noin 200 vuotta sitten. Eli miten voisi saada kokoonpanon onnistumaan ilman, että osia tarvitsee sovittaa paikalleen joka kerta tuotannossa tai rikkoutuneita osia kentällä vaihtaessa. Ratkaisu oli lopulta toleranssit ja tarkastus, eli osien toimittaja huolehti, että osien vaihtelu on sovitulla välillä. Tämä tarkoitti käytännössä erilaisten tulkkien käyttöä. Ihan heti ei ymmärretty miten tämä toimi, mutta se mahdollisti monimutkaisten laitteiden valmistuksen edullisesti. 

Nykyään, noin 200 vuotta myöhemmin tarkastuksesta on luovuttu tehottamana menetelmänä ja on siirrytty poistamaan osien ongelmat ennen kuin niitä toimitetaan tai edes tuotetaan. Alun perin autoteollisuudesta sovelletun hyväksymismenettelyn perustarkoitus on antaa ostajalle riittävä luottamus siitä, että tilatut komponentit tai osat ovat heidän vaatimusten mukaisia niin, että toimittajan tekemiset eivät aiheuta ostajan tuotannolle tai lopputuotteelle liiallista riskiä. Olettamuksena tietenkin on, että itse toleranssi on osattu määrittää oikein, eikä niistä tarvitse huolehtia.

PPAP on parhaimmillaan erittäin kattava todistusaineiston nippu ja tietynlainen oletus siis on, että nämä tiedot vain ”kaapataan” toimittajan laadunhallintajärjestelmästä, koska ne ovat perusasioita ja menetelmiä, joita käytetään lähes päivittäin osana autoteollisuuden pitkää valmistusketjua. 

Näin ei kuitenkaan välttämättä ole autoteollisuuden suorien vaatimusten ulkopuolella ja pahimmillaan tätä näyttöä aletaan rakentamaan, kun osat on jo toimitettu tai valmistettu. Näin ollaan hullunkurisessa tilanteessa, jossa tehdään asioita vain koska jossain niin vaaditaan. Vaikka menetelmät ja analyysien tulkinta olisi organisaatiossa hallussa, johdon tulisi varmistaa niiden oikea-aikainen soveltaminen!

Riittävän suorituskyvyn varmistaminen on oman toiminnan kannalta tuotannon ulostuloa häiritsevän keskeisen hukan, eli uudelleen tehtävän työn (rework) vähentämisestä tai eliminoimisesta. Jos kokoonpanon tai valmistuksen mahdollisuuksia onnistua ensimmäisellä kerralla lisätään, on mahdollista lisätä ulostuloa samassa ajassa. Usein on ymmärretty vaihtelun pienentämisen merkitys systeemin ulostulon kannalta ja kokoonpanossa tämä on hyvin konkreettinen asia. 

Suorituskyky ja stabiilisuus

Yksi läntisen autoteollisuuden (IATF 16949-standardi) ajamista keskeisistä vaatimuksista koko toimitusketjulle tai verkostolle on tärkeiksi määriteltyjen ominaisuuksien suorituskyky. Yksinkertaistettuna tämän on toleranssin ja havaitun vaihtelun välinen suhde. Tästä käytetään joskus myös termiä prosessin laaduntuottokyky, englanniksi process capability. Keskeinen ehto suorituskyvylle on, että prosessiin vaikuttaa ainoastaan satunnaiset syyt, jolloin sen vaihtelu on ennakoitavaa (stabiilia).

Suomeksi laaduntuottokyky tarkoittaa kappaleen tai prosessin mitattavien ominaisuuksien hajontaa, jonka pitäisi olla riittävästi vaatimusten sisäpuolella, mielellään keskellä suunnittelun määrittämää toleranssialuetta. Ei siis riitä, että osat ”on spekseissä” vaan tulee näyttää, että valmistetut osat pysyvät ennustettavasti tavoitearvon ympärillä ja vaihtelu on ohjauksessa. Suorituskyky ilmaistaan suorituskykyindeksillä, joita on hämmentävästi erilaisia, mutta niiden yksinkertaisin muoto on C_p, joka kertoo tavoitteen ja hajonnan suhteen. 

Suorituskykyindeksin (C_p) peruskaava on esitetty alla.

Joskus kysytään, että miksi näin vaikea käsite kuin suorituskykyindeksi on käytössä. Onko sillä tarkoitus huijata hankintaa ja hämmentää ostoa?

Yksi keskeinen syy on, että näin ei joka kerta ei tarvitse keskustella toleransseista ja hajonnasta, vaan tilanteen kuvaamiseen riittää yksi tai muutama luku. Arvot alle suunnitellun tason (kuten 1,67 tai vastaava) kertovat tarpeesta prosessin ohjauksien kehittämiselle, johon alihankkija on tietenkin sitoutunut ja tietää kuinka toteuttaa. Autotehtaan mielenkiintoina on, että virheellisten komponenttien määrä on erittäin alhainen, koska muuten tuotetta ei saada kasattua tai toimitusaikaa ei voi ennustaa kukaan.

Suorituskyvyn ajatus on siis hyvin yksinkertainen tapa kertoa, onko epäonnistuminen mahdollista tai onko meillä riskiä. Jos indeksi on 1, täyttää prosessi koko vaihtelulle varatun toleranssin alueen. Jos indeksi on 2 niin toleranssialueesta täytetään vain puolet, eli riski toleranssien ylityksille ja poikkeamille asiakkaalla on huomattavasti pienempi. 

Voisi ajatella, että prosessilla on liikkumavaraa, jolloin kokoonpanossa ei pitäisi olla komponenttien sovittamista, paikalleen vasarointia tai vastaavaa hukkatyötä, ellei kyseessä ole erityinen syy. Ollaan siis ”nollavirheen” alueella ja komponentit mahdollistavat omalta osaltaan kokoonpanon siihen varatussa ajassa. Huomattavaa on, että nollavirhettä ei virheiden kautta oikeastaan voida mielekkäästi mitata tai osoittaa järkevillä näytemäärillä.

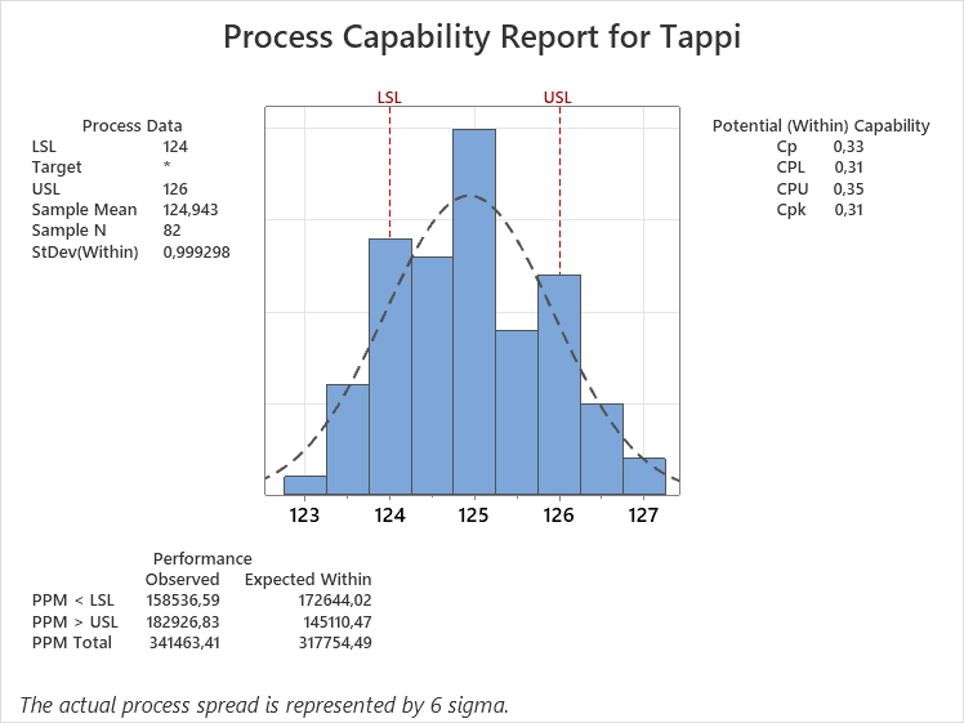
Kuvassa 3 on esitetty tyypillisen suorituskykyanalyysin elementit Minitab-ohjelmalla komponentin kriittiseksi tiedetyn halkaisijan mitoista. Toleranssit ovat 125 ja 126, tai 125+/-1 yksikköä kuten ne usein ilmaistaan. Suorituskykyindeksi C_p on 0,33 ja koska mitta on hyvin keskitetty ei eroa muihin indekseihin käytännössä ole (näistä seuraavaksi alla).  

Alareunassa Minitab näyttää havaitut (observed) toleranssien ylityksien määrät per miljoonaa osaa (PPM) jaoteltuna ylätoleranssiin (USL) ylittäviin ja alatoleranssiin (LSL) alittaviin. Näiden vieressä esitetään sovitetun jakauman perustella tehty ennuste tai odotus ylityksistä (expected), perusasetuksilla tässä nähdään myös kokonaishajonnalla tehty ennuste. Nämä voi halutessaan myös vaihtaa PPM-luvuista prosenteiksi, jos prosentin desimaalit ovat vielä käyttökelpoisia. Näin ihmisten yleensä helpompi hahmottaa tilannetta, vaikkakin luvut ovat edelleen ihan samoja.

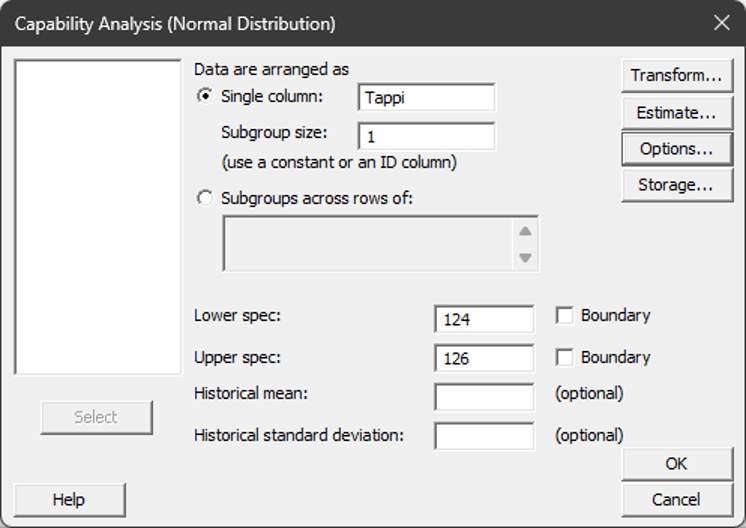
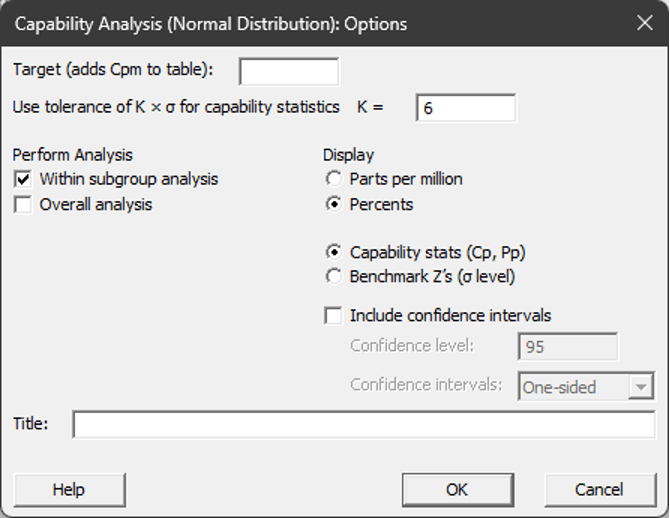
Kuva 4. Minitab kyvykkyysanalyysin dialogi (Stat>Quality Tools> Capability Analysis>Normal) ja PPM vaihto prosenteiksi Options dialogista.

Yllä (kuva 4) on esitetty Minitab-dialogin valinnat prosenteille ja perusanalyysin tekeminen. Näistä oleellista on tietää datan keräyksen alaryhmän tai näyteryhmän koko (subgroup size). Jos havainnot ovat yksittäisiä, eikä esimerkiksi yhden muotin tai muun luonnollisen alaryhmän tuotosta, tähän tulee laittaa 1, eli yksittäisiä havaintoja. Ilman lukua kentässä, ei analyysiä voi ajaa.

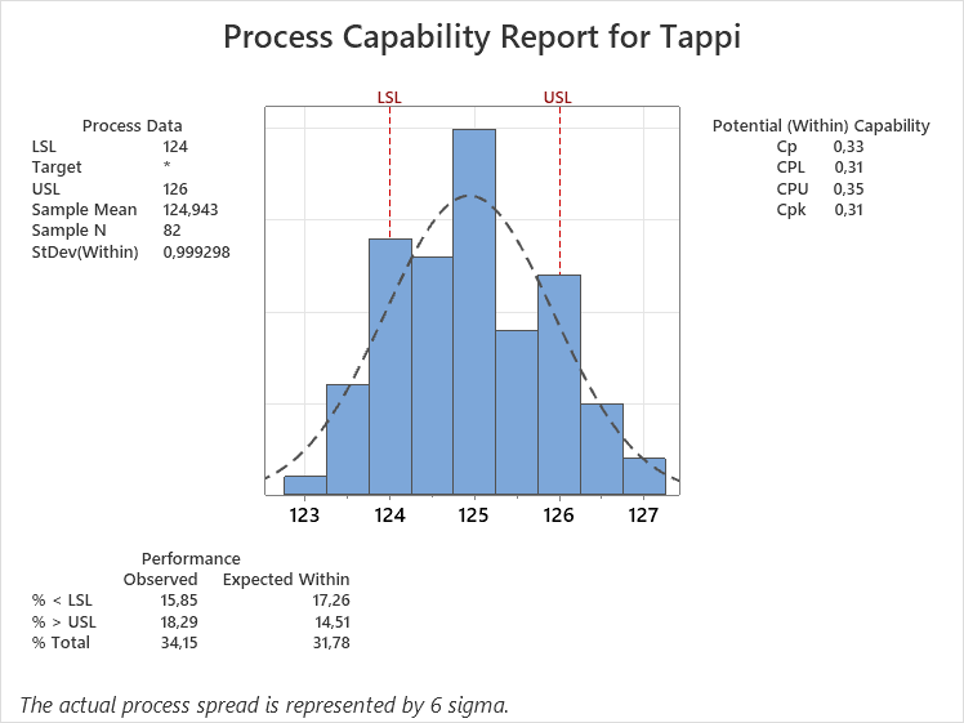
Tämän analyysin oletuksena on normaalijakautunut data (tässä pitää paikkansa), johon perustuu myös tehty ennuste huonon määrästä tulevaisuudessa (31,78%). Lisäksi vaihtelun tulee olla ohjauksessa, eli prosessiin ei saa vaikuttaa erityiset syyt, jota ei tästä kuvasta voi nähdä, mutta tiedetään pitävän paikkansa.

Huomattavaa on, että nämä ehdot eivät ole varsinaisesti toisiaan poissulkevia, mutta jos normaalisuuden ehto ei täyty syynä voi olla erityiset syyt tai merkittävät poikkeamat. Epänormaalisuus voi olla tavallista jostain luonnollisesta syystä (vinot jakaumat), jolloin tulisi käyttää tarkoitukseen sopivaa analyysiä, jotta ei ali- tai yliarvioida todellista suorituskykyä. 

Erot indekseissä

Vaikka suorituskyvyn ajatus on suhteellisen yksinkertainen, keskustelua hämmentää sen ilmaisussa käytetyt erilaiset kirjainyhdistelmät ja indeksit, sekä lyhyen ja pitkän ajan suorituskyvyn termit. Nämä eivät ole itsestäänselvyyksiä, eikä niiden merkitystä ja ymmärrystä pitäisi jättää pelkästään suunnittelu- tai valmistusosaston sisälle.

C-ja P-indeksien ero on tavassa, jolla keskihajonta (sigma) määritetään. Näiden yhteydessä käytetään myös lyhyen ja pitkän ajan prosessin kyvykkyyden tai näytteen käsitteitä. Käytännössä C-indekseissä hajonta lasketaan käyttäen näyteryhmien sisäistä hajontaa, kun P-indekseissä käytetään koko datajoukon kokonaishajontaa. Tämä kuulostaa varsin hienolta, mutta mikä on tämän tarkoitus ja merkitys käytännössä?

C-alkuisissa hajontana on keskihajonta, joka on arvioitu huomioiden näyteryhmien sisäinen vaihtelu, kun P-alkuiset (Performance) käyttävät koko tutkimuksessa käytetyn datajoukon keskihajontaa. Tämä on aina huonompi kuin ”lyhyen ajan” datasta saatava arvio, koska mahdolliset tuotantoerien ja asetusten väliset keskiarvotasojen vaihtelut tulevat mukaan antaen siten realistisemman kuvan asiakkaalla tai omassa kokoonpanossa havaitusta vaihtelun määrästä. Jos P ja C indeksien ero on suuri, kertoo se heikosta kyvystä ohjata prosessia esimerkiksi tuotantoerien välillä.

Taulukko 1. Suorituskykyindeksien erot

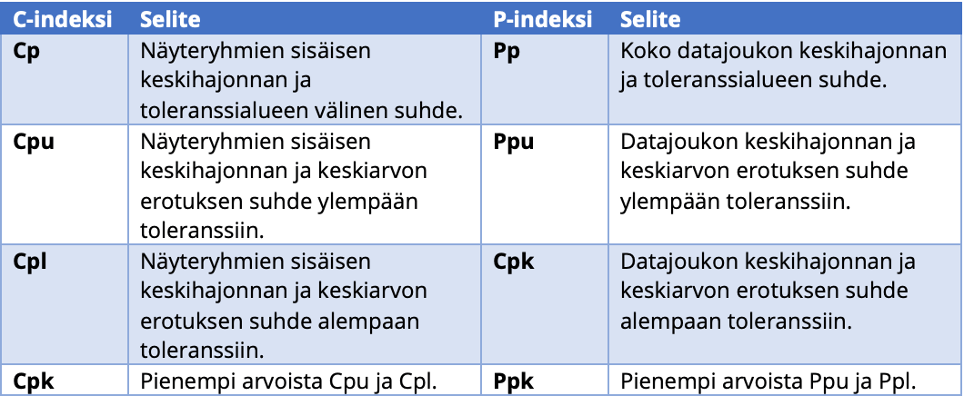
Taulukossa 1 on koottu C ja P indeksien erot sanallisessa muodossa. Aiemmin kuvattu C_p-indeksi ja sen vastinpari P_p kuvaavat siis toleranssin ja prosessin (tai komponentin ominaisuuden) vaihtelun suhdetta. Ne eivät ota kantaa siihen, miten prosessi on keskittynyt toleranssialueen sisälle. Joten näiden avulla voidaan tarkastella prosessin potentiaalista suorituskykyä, eli mitä saadaan, jos keskiarvo saadaan säädettyä keskelle toleranssialuetta, missä se ei välttämättä tällä hetkellä ole. 

Ilman datan tarkastelua ja analysointia voidaan siis tehdä arvio toimittajan kyvystä valmistaa tasalaatuisia komponentteja viikosta viikkoon ja toimituksesta toimitukseen, mikä on tietysti kaikenlaisessa toiminnassa äärimmäisen käytännöllistä.

C_p ja P_p ovat sokeita prosessin paikalle, joten prosessin keskiarvon ongelmat tulee päätellä muista indekseistä, joista yleensä tarkastellaan yleensä vain pienemmän luvun ilmoittavaa indeksiä C_pk tai P_pk. Jos on käytössä kuva itse hajonnasta, on yleensä helppo nopeasti päätellä, onko keskiarvo liian suuri tai pieni, mutta indeksejä tarkastelemalla se toki onnistuu ”sokeanakin”. Kuvassa 6 alla on esitetty tilanne, jossa on ilmeinen keskiarvon paikan ongelma.

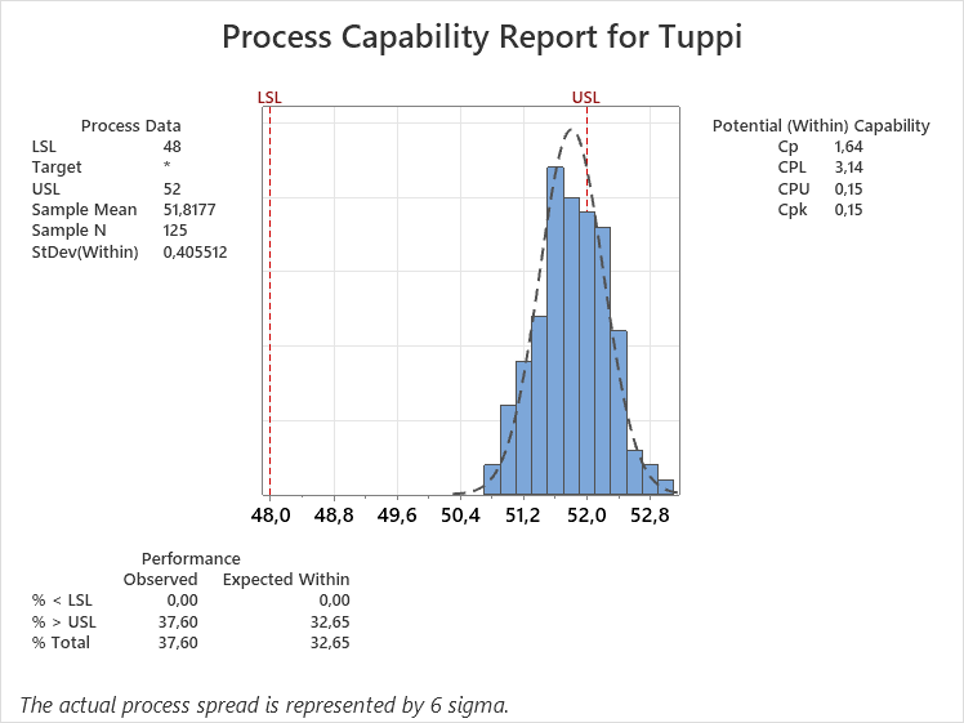
Kuvan 6 johtopäätökset voitaisiin tehdä pelkillä indekseillä, mutta kuva auttaa ymmärtämään nopeammin mistä on kyse.

Tämänkaltainen prosessin tai komponentin mittojen keskittyminen toiseen laitaan tai koko toleranssin leveyden käyttö kertoo ohjauksen kypsymättömyydestä, eli että prosessia ei ole pystytty suunnitelmaan vastaamaan asiakkaan vaatimuksiin, tai että sitä ei ohjata oikealla tavalla. Kuvan tapainen tilanne ei ole harvinainen, jos on totuttu tekemään vähän isompaa, josta jää sitten sovittamisvaraa.

Voisi siis ajatella, että on puute tiedossa, mitä tulee ohjattaviin kohteisiin tai ohjauksen toteuttamiseen. Tämä näkyy indekseissä C_pu, C_pl sekä niiden vastinpareissa P_u ja P_pl, jotka kukin käsittelevät suhdetta keskiarvon ja ylemmän (u=upper) tai alemman (l=lower) toleranssin ja prosessin hajonnan suhteen. Näistä huonompi tilanne esitetään indekseissä C_pk tai vastaavasti P_pk.

Sixpack näyttää kaiken oleellisen kerralla

Kun halutaan nopeasti saada selville tai näyttää kaikki oleelliset kuvat ja analyysit valitusta komponentin mitasta tai prosessin mittarista, on Minitab Capability Six Pack varsin hyödyllinen kuvakooste.

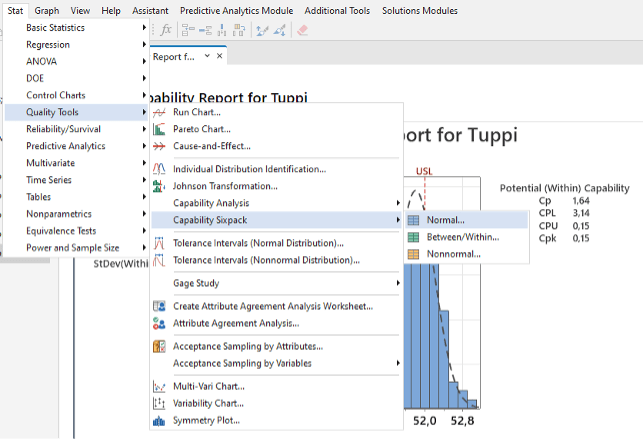
Kuvassa 7 on näytetty analyysin paikka Minitab-valikossa. Vastaavan analyysin voi tehdä näppärästi myös Assistant valikon kautta.

Valittaessa oikeaa työkalua on tieto käytettävästä jakaumasta oleellista, mutta on tyypillistä, että erilaiset fyysisten kappaleiden mitat ovat normaalista jakautuneita. Mutta toki poikkeuksiakin on, jolloin tulisi käyttää sopivaa jakaumaa ja valita Nonnormal vaihtoehto. Normaalisuuden rikkominen saattaa myös tarkoittaa, että toimittaja tekee erottelua, tarkastusta tai keksii mittaustuloksia, joten ole tarkkana, jos jakauma näyttää ”leikatulta”.

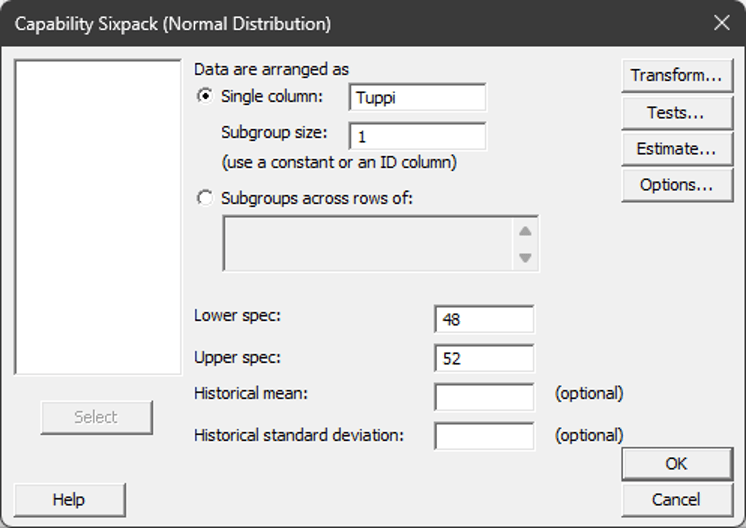
Varsinainen dialogi Sixpackissä on samanlainen kuin varsinaisessa yksittäisessä kyvykkyysanalyysissä, joten sinun pitää tietää toleranssit (tai toinen niistä), sekä datan alaryhmän koko (yksittäisillä havainnoilla 1). Kuvassa 8 on esitetty dialogin täyttö esimerkkidatalla.

Kuvassa 9 (alla) on varsinainen dialogin tuotos, jossa nähdään sama jakauman kuva kuten aikaisemmassa analyysissa (oikea ylänurkka). Tällä kertaa histogrammiin on sovitettu normaalijakaumat, molemmilla keskihajonnan arvioilla, sisäisen vaihtelun (within, katkoviivalla) ja koko datajoukolla (overall, punaisella). 

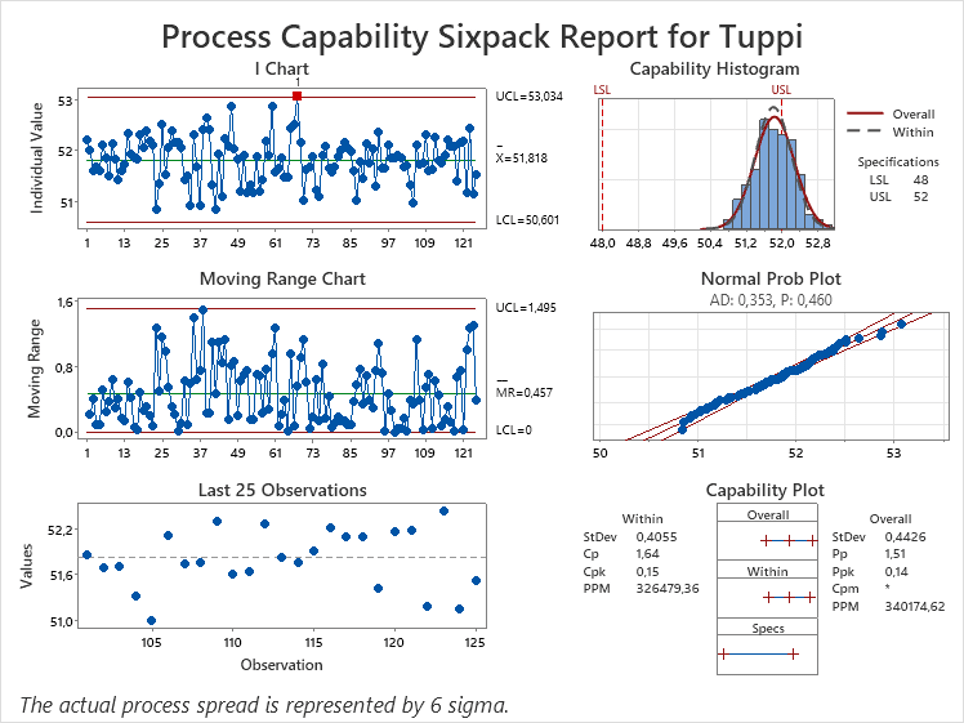
Tässä tilanteessa jakaumat ovat käytännössä päällekkäisiä, koska mittojen vaihtelu on yhdenmukaista koko näytteen ajalta, eikä Sixpack-kuvan ohjauskorteissa ole näyttöä, että prosessin keskiarvo siirtyisi tai vaihtaisi paikkaa missään vaiheessa. Tämä näkyy myös siinä, että C ja P-indeksit ovat lähellä toisiaan.

Jos data on kerätty alaryhmissä, tulee yksittäisten havaintojen (I-chart) tilalle keskiarvokortti ja liukuvan vaihteluvälin (MR) tilalle, näyteryhmän koon mukaan vaihteluvälin (R, range) kortti tai keskihajonnan (S, sigma) kortti. Huomattavaa, että ohjauskorttien rajat ovat prosessin tilastollisen stabiilisuuden tai satunnaisuuden rajat, eivätkä tuotteen tai prosessin speksit, kuten histogrammissa.

Sixpackin normaalisuuskuva ja sen yläpuolella oleva hypoteesitesti on tarkoitettu varmistamaan, että datasta tehtävä normaalisovitus ja siitä tehtävä ennuste olisi mielekäs. Kuten kaikissa histogrammeissa, ohjelmisto tekee työtä sille annetuilla parametreilla ja jos data ei täytä ehtoja, ei sovitus ja siitä tehtävät arviot ole järkeviä. Tässä normaalisuusehto täyttyy, sillä pisteet osuvat 95% luottamusvälille ja testin P-arvo on yli 0,05. Tällä testillä ei ole siis mitään tekemistä stabiilisuuden kanssa, vaikka näin joskus väitetään. Toki jos jokin on perinteisesti normaali ja muuttuu yllättäen epänormaaliksi, tulisi syy selvittää ja koittaa ymmärtää mistä tämä johtuu.

Huojuva prosessi

Tyypillinen ongelma kaikenlaisen metallin jalostamisen, muovin puristamisen tai komponentin valmistuksen maailmassa on, että toimitettujen erien välinen vaihtelu on suhteellisen pientä, mutta ongelmat alkavat erän vaihtuessa. Eli ongelma on erien välisen vaihtelun ohjauksessa tai säädöissä. Tämä näkyy suorituskykyanalyysissä merkittävänä erona juuri C-ja P-indeksien välillä ja kiinteän ja katkoviivalla ilmaistun hajontasovituksen eroina Minitabissa.

Tallaista tilannetta on kuvattu alla kuvassa 10, jossa vaihtelu kokonaisdatassa on noin puolet suurempaa kuin yksittäisten mittausten välinen vaihtelu.

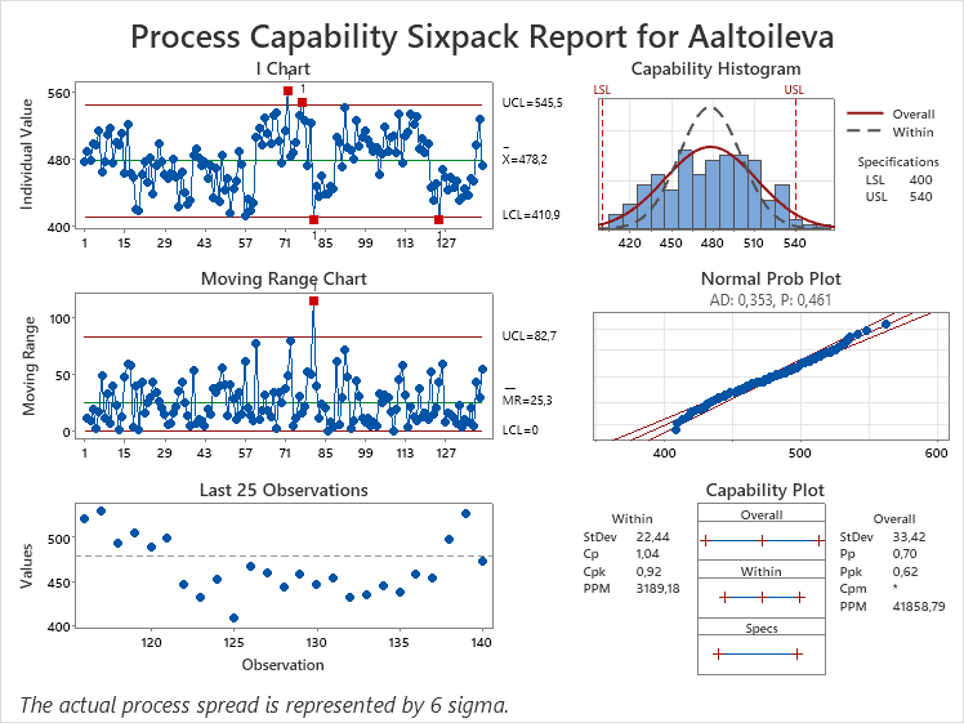
Nyt C_p ja P_p -indeksien välillä on jonkinlaista eroa, joka voidaan havaita myös ohjauskortista (oikea yläkuva). Indeksien erosta voidaan nähdä potentiaali, mitä voidaan saada eliminoimalla erien keskiarvojen välinen vaihtelu, joka voi tulla esimerkiksi eri materiaaleista, asetuksista, vuoroista tai mistä tahansa prosessiin vaikuttavasta erityisestä syystä.

Eli jos näiden aiheuttama vaihtelu voitaisiin eliminoida, päästäisiin lähemmäksi C_pk-indeksiä 0,94. Vastaavasti jos keskiarvo saataisiin toleransseihin nähden paikalleen, voitaisiin saada irti potentiaalinen 1,04. Tämä ei tietenkään ole kovin hääppöinen, mutta huomattavasti parempi kuin nykyinen noin 40 % virheellisten taso. 

Huomattavaa kuitenkin on, että tässä vaihtelun syiden selvittäminen erien välisten erojen vaihteluiden ohjaamiseksi mahdollistaisi merkittävän onnistumisen tason noston ilman investointeja. Kapasiteettia lähes ilmaiseksi pelkällä päättelyn, analyysin ja aivotyön voimalla!

Älä hyväksy näytekoon taakse piiloutumista

Usein perusteelle jättää suorituskyky huomioimatta tai selvittämättä, esitetään että:

 ”Meidän tuotanto on niin pientä, että mielekästä näytemäärää joutuu odottamaan vuosikausia” 

Tämä saattaa olla osittain totta, kun ajatellaan että autoteollisuuden PPAP-menettely yleensä vaatii 300 kappaleen tuotantoajon, josta itse todennus riittävästä laadusta haetaan. Tämä ei tarkoita, etteikö suorituskykyanalyysiä voisi tai pitäisi silti soveltaa muissa tilanteissa.

Käytännössä suuri näytemäärä on perusteltua mielekkäiden luottamusvälien arvioimiseksi. Eli koska kyseessä on vain näyte, onko alempi luottamusväli tarpeeksi korkealla, että voimme luottaa hajonnan olevan riittävää. Tämä on suurissa volyymeissä tietenkin ymmärrettävä huoli, koska riski on suuri loppukäyttäjälle ja omalle toiminnalle.

Suorituskykyanalyysiä voidaan kuitenkin tehdä pienemmilläkin näytteillä, autoteollisuuden PPAP-manuaali antaa ohjeistusta ja poikkeamia juuri pienten volyymien tuotantoa ja näytekokoa varten. 

Toinen vaihtoehto on siirtyä komponenttitasolta prosessitasolle ja tarkastella hajontaa prosessin ulostulon kannalta, eli keskittyä prosessiin pelkän tuotettavan osan tai komponentin mitan sijasta.

Ei tulisi kuitenkaan hyväksyä ajatusta, että tilastollisten menetelmien soveltaminen vaatii suuria satojen tai tuhansien mittaustulosten kasaamista ja analysointia. Tulisi ymmärtää, että pienempien datajoukkojen tulkinnassa ja johtopäätöksissä on vain enemmän epävarmuutta, mutta se ei ole este ennakoivien menetelmien käytölle. 

Tarkoitus on mahdollistaa onnistuminen omassa tai tai asiakkaan tehtaassa ja varmistaa loppukokoonpanon toimivuus asiakkaan käytössä!